1) 18см
2) 12см
3) 6см
4) 27см.
Найдите стороны четырехугольника.
Объяснение:
Пусть длина 1 стороны - х см.
Запишем % в десятичном виде:
50%=50/100=0,5
150%=150/100=1,5
1 сторона - х см
2 сторона - 2/3х
3 сторона - (2/3х)×0,5
4 сторона - 1,5х
Р (периметр) - 63 см
1)Составим уравнение:
х+2/3х+(2/3х)×0,5+1,5х=63
х+2/3х+(2/3)×(1/2)х+3/2х=63
х+2/3х+1/3х+3/2х=63 | ×6
6х+4х+2х+9х=63×6
21х=378
х=378:21
х=18 см первая сторона;
2) 18×2/3=12 (см) вторая сторона;
3) 12×0,5=6 (см) третья сторона;
4) 18×1,5=27 (см) четвертая чторона.
1 сторона 18 см
2 сторона 12 см
3 сторона 6 см
4 сторона 27 см.
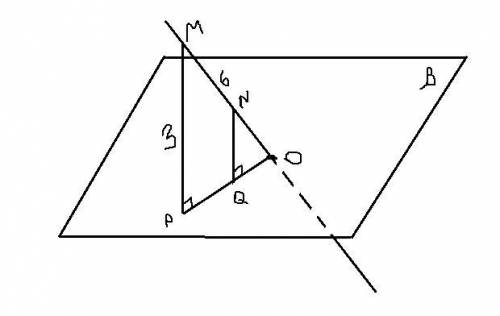
1см
Объяснение:
Точка N может лежать по одну сторону от плоскости β с точкой М или по другую. Если N лежит по другую сторону, то невозможно выполнить условия MN = 6 см и при этом OM = 9 см. Поэтому рассматриваем только случай, когда M и N находятся по одну сторону от плоскости β.
В этом случае расстояние от M до плоскости (определяется перпендикуляром, опущенным на эту плоскость) равно PM=3см. А расстояние от N до плоскости - QN.
Рассмотрим тр-ки MPO и NQO. Они подобны (2 угла прямые, а ещё один угол MOP общий). Значит PM/QN=OM/ON. ON=9-6=3
QN=PM*ON/OM=3*3/9=1
Докажем свойство пропорциональности хорд.
A=K (вписанные углы, опирающиеся на дугу MB)
△APM~△KPB (по двум углам)
AP/KP=PM/PB <=> AP*PB=KP*PM
Диаметр, перпендикулярный хорде, делит ее пополам (△KOM - равнобедренный, OP - высота и медиана).
KP=PM =x
x^2 =6*8 <=> x=4√3
KM=2x =8√3