ответ: а) 40°, 70°, 70°. б) 40°, 40°, 100°.
Задача имеет два решения.
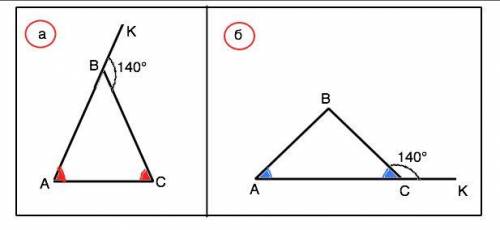
а) Дан внешний угол при вершине В, противолежащей осноанию. Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
По условию ∆ АВС - равнобедренный. Поэтому ∠А=∠С=140°:2=70°.
б) Данный внешний угол - смежный с одним из внутренних углов при основании треугольника АВС. Развернутый угол АСК равен сумме смежных углов = 180°. ⇒ угол ВСМ=180°-140°=40°
∠ВАС=∠ВСМ=40°
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним. Угол ВАС+СВА=140° ⇒ ∠АВС=140°=40°=100°
Объяснение:
Поскольку точка К является серединой отрезка EF, то из формулы деления отрезка пополам, имеем:
XK = (XE + XF / 2
Отсюда:
XF = 2·XK - XE = 2·0 - (-1) = 1.
Аналогично:
YF = 2·YK - YE = 2·0 - 2 = -2;
ZF = 2·ZK - ZE = 2·2 - 4 = 0.
Итак:
F (1; -2; 0)