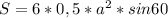, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 
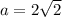. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
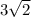. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
площадь прямоугольного треугольника = половине произведения его катетов (a и b)...
ab/2 = 24 => ab = 48
a-b = 2 => a = 2+b
(2+b)b = 48
b^2 + 2b - 48 = 0
D = 4+4*48 = 4*49
b(1;2) = (-2+-2*7)/2 ---отрицательный корень не имеет смысла...
b = -1+7 = 6
a = 8
т.к. точка равноудалена от вершин треугольника, т.е. все наклонные из точки к плоскости (к вершинам треугольника) равны, то равны и проекции этих наклонных, т.е. точка проецируется в центр описанной около треугольника окружности.
для прямоугольного треугольника известно, что центр описанной окружности лежит на его гипотенузе и радиус описанной окружности = половине гипотенузы...
по т.Пифагора найдем гипотенузу
c^2 = 6^2 + 8^2 = 36+64 = 100
c = 10
и еще раз по т.Пифагора
искомое расстояние = корень(12^2 + 5^2) = корень(144+25) = 13