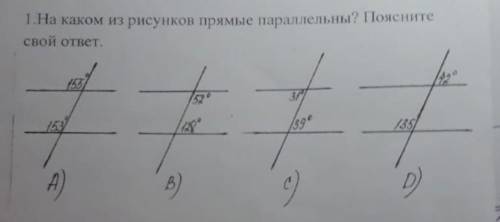
На каком из рисунков прямые параллельны? поясните свой ответ

Question

Геометрия: На каком из рисунков прямые параллельны? поясните свой ответ​

Random00700 · Accepted Answer

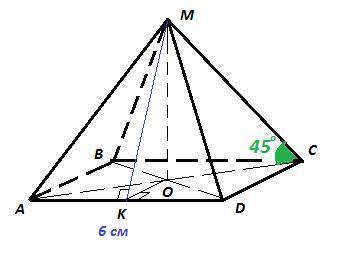
Пирамида MABCD - правильная, в основании лежит квадрат ABCD,

AB=BC=CD=AD=6 см, боковые рёбра равны AM = BM = CM = DM, высота опускается в точку пересечения диагоналей квадрата.

Диагональ квадрата равна d = a√2 :

AC = AB · √2 = 6√2 см

Диагонали квадрата точкой пересечения делятся пополам :

OC = AC : 2 = 6√2 : 2 = 3√2 см

ΔMOC - прямоугольный равнобедренный, так как

∠CMO = ∠MCO = 45° ⇒ OM = OC = 3√2 см

MK - апофема боковой грани AMD

ΔMOK - прямоугольный, KO = AB:2 = 6:2 = 3 см

По теореме Пифагора

MK² = OM² + KO² = (3√2)² + 3² = 18 + 9 = 27

MK = √27 = 3√3 см

Sбок = 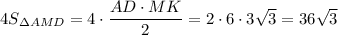$4S_{\Delta AMD}=4\cdot \dfrac{AD\cdot MK}2=2 \cdot 6 \cdot 3\sqrt 3=36\sqrt3$ см²

ответ : 36√3 см²

На каком из рисунков прямые параллельны? поясните свой ответ​