Ну, первая проще некуда - умножаем 4*6 - это площадь одной боковой стороны, и еще умножаем на 4(стороны) Итого 4*6*4=96см^2
2. по апофеме и высоте вычисляем половину длины стороны основания пирамиды. Это по формуле (10^2-8^2) и все это под корнем. получается 6, еще умножаем на 2=12 (сторона основания)
далее вычисляем площадь по формуле: S=(1/2)PL+Sосн, где Р-периметр основания (12*4=48), L-апофема, Sосн-площадь основания (12*12=144). Итого (1/2)*48*10+144=384см^2
3 не знаю до конца, можно вычислить верхние и нижние диагонали по той же формуле, что и в пред. задаче, получается 8корней из 2 и 18корней из 2 соответственно. Если найдешь высоту усеченной пирамиды, можно будет узнать площадь сечения.
KB = 10
Объяснение:
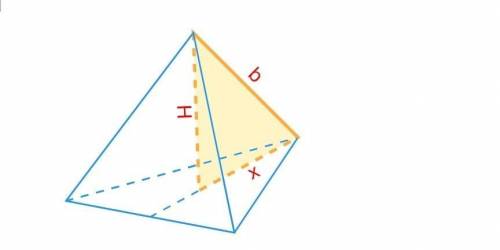
Судя по описанию, это - правильная треугольная пирамида.
Нам нужно найти боковое ребро пирамиды
(см. рисунок)
Для начала найдём расстояние от центра треугольника, до любой из его вершин с формулы для нахождения радиуса описанной около правильного треугольника окружности:
R=a/√3 , где a - сторона, равная по условию 6√3
Подставляем R=6√3/√3 = 6 - наш нижний катет прямоугольного треугольника KOB(к примеру)
Теперь нам известны два катета: KO или высота = 8,
OB = 6
Найдём гипотенузу KB с теоремы Пифагора:
KB=√(6²+8²) = √(36+64) = √100 = 10
Объяснение:
3 надо угла