V= 4/3*πR³ = 4/3*π*(√3)³ = 4π√3
Чертёж смотрите во вложении.
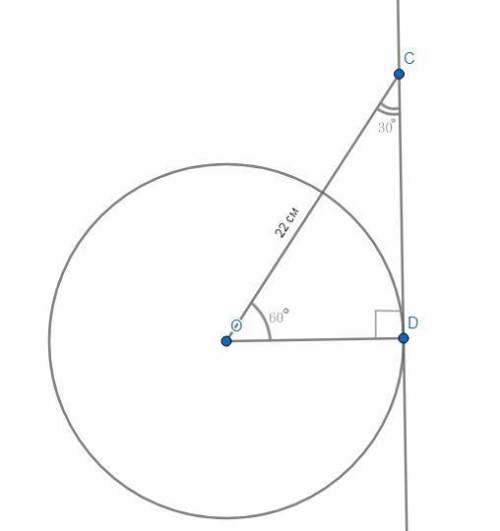
Дано:
Окружность с центром О.
CD - касательная.
D - точка касания.
OD - радиус.
ОС = 22 см.
∠COD = 60°.
Найти:
ОD = ?
Радиус, проведённый в точку касания перпендикулярен этой касательной. Следовательно, ΔCOD - прямоугольный.Рассмотрим ΔСOD - прямоугольный. ∠OCD = 90°-∠COD = 90°-60° = 30° (так как сумма острых углов прямоугольного треугольника равна 90°). Против угла в 30° лежит катет, равный половине гипотенузы. В нашем случае гипотенуза - СО, так как лежит против угла в 90°. OD - тот самый катет, лежащий против угла в 30°. Поэтому, OD = 0,5*СО = 0,5*22 см = 11 см.ответ: 11 см.
Объяснение:
О - точка пересечения диагоналей ВD и АС. ВО/OD=2/5. h=BC=4
1) Тр-ки ВОС и AOD подобны по трем соответственно равным углам (1 пара вертикальных и 2 пары накрест лежащих). Из подобия следует пропорциональность сходственных сторон: BC/AD=BO/OD; AD=BC*OD/BO=4*5/2=10.
2) Проведем две высоты ВN и СМ. Высоты разделят нижнее основание на отрезки;
NM=BC=4; AN=MD=(AD-NM)/2=3.
3) Тр-к ABN с катетами BN=4 и AN=3 - египетский. Значит, гипотенуза АВ=5. (А можно найти АВ по теореме Пифагора),
4) Р=2*АВ+BC+AD=10+4+10=24 см.
Объем шара V= 4ПR^3/3 = 4П*√3^3/3 = 4П √3