Мальчик-школьник теряется в тайге и выходит к заповедному озеру, полному рыбы. Найдя дорогу домой, он приводит к новому месту рыболовную бригаду своего отца, после чего озеро называют его именем.
Рыбакам из бригады Григория Афанасьевича Шадрина, Васюткиного отца, не везло. Вода в реке поднялась, и рыба ушла на глубину. Вскоре с юга подул тёплый ветер, но уловы оставались небольшими. Рыбаки отошли далеко в низовья Енисея и остановились в избушке, построенной когда-то учёной экспедицией. Там и остались ждать осеннюю путину.
Рыбаки отдыхали, чинили сети и снасть, ловили рыбу перемётами, а Васютка каждый день ходил за кедровыми орехами — очень уж любили рыбаки это лакомство. Иногда мальчик заглядывал в новые учебники, привезённые из города, готовился к школе. Вскоре шишек на ближайших кедрах не осталось, и Васютка решил отправиться в дальний поход за орешками. По старинному обычаю мать заставила мальчика взять с собой краюшку хлеба и спички, а без ружья Васютка никогда в тайгу не ходил.
Доказательство теоремы Пифагора
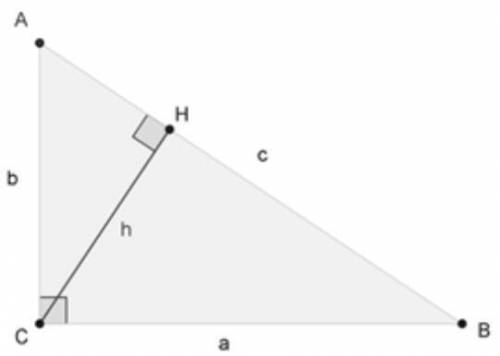
Пусть треугольник ABC - прямоугольный треугольник с прямым углом C
Проведём высоту из вершины C на гипотенузу AB, основание высоты обозначим как H .
Прямоугольный треугольник ACH подобен треугольнику ABC по двум углам ( ∠ACB=∠CHA=90∘∠ACB=∠CHA=90∘, ∠A∠A - общий). Аналогично, треугольник CBH подобен ABC .
Введя обозначения
BC=a,AC=b,AB=cBC=a,AC=b,AB=c
из подобия треугольников получаем, что
ac=HBa,bc=AHbac=HBa,bc=AHb
Отсюда имеем, что
a2=c⋅HB,b2=c⋅AHa2=c⋅HB,b2=c⋅AH
Сложив полученные равенства, получаем
a2+b2=c⋅HB+c⋅AHa2+b2=c⋅HB+c⋅AH
a2+b2=c⋅(HB+AH)
AB=(0,5; 1; -1) |AB|=1,5
BC=(0;-2;2) |BC|=2
AC=(1/2;-1;1) AC|=1.5
P=5
m=sqrt(1+2,25)=sqrt(3.25)
(1/4;-1,5;1.5)
m=sqrt(2,25+2,25+1/16)
m=sqrt(73)/4