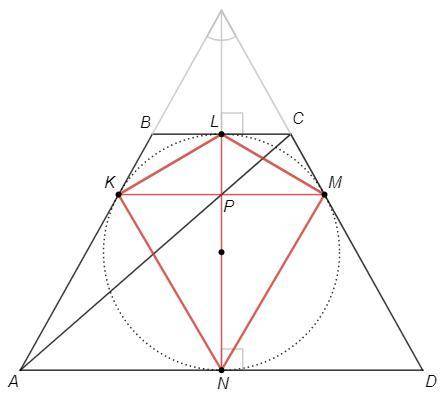
Достроим трапецию до равнобедренного треугольника.
Центр вписанной окружности лежит на биссектрисе.
Биссектриса к основанию является высотой и медианой.
Окружность касается оснований в серединах.
BL=CL, AN=DN
Отрезки касательных из одной точки равны.
BK=BL=CL=CM =a
AK=AN=DN=DM =b
По теореме о пропорциональных отрезках KM||BC||AD
△KAP~△BAC, KP/BC=AK/AB => KP/2a =b/(a+b)
△PCM~△ACD, PM/AD=CM/CD => PM/2b =a/(a+b)
KP=PM =2ab/(a+b)
LN - высота => LN⊥KM
S(KLMN) =1/2 KM*LN *sin90 =2ab/(a+b) *LN
S(ABCD) =1/2 (AD+BC)*LN =(a+b) *LN
S(ABCD)/S(KLMN) =(a+b)^2/2ab =8/3 =>
(a^2 +b^2 +2ab)/2ab =8/3 =>
a/2b +b/2a +1 =8/3 =>
a/b +b/a =2(8/3 -1) =10/3
a/b =x
x +1/x =10/3 =>
x^2 -10/3 x +1 =0 => x = {1/3; 3}
ответ: основания относятся 1:3
площадь полной поверхности = площади боковой поверхности + 2 площади основания.
1) в оснвоании лежит прямоугольный треугольник. площадь находим как 1/2 произведения катетов , т..е 12*5: 2= 30 см^2/
2)площадь бококвой поверхности = половине периметра основания на высоту.
чтобы найти периметр , надо знать все три стороны треугольника. треугольник прямоугольный, поэтому гипотенузу находим по теореме пифагора. 12^2+5^2=144+25=169, гипотенуза равна 13.
3) ищем периметр 13+12+5=30 см.
4) ищем площадь боковой поверхности 30*10=300
5) площадь полной поверхности равна 300+2*30=360 см
подробнее - на -
60°
Объяснение:
Катет RS равен половине гипотенузы SQ, что видно из условия, значит, RS лежит против угла 30°, ∠Q=30°.
Cумма острых углов прямоугольного треугольника составляет 90°, поэтому ∠S=90°-30°=60°.