1 ) В основании пирамиды лежит квадрат. Одна из боковых граней пирамиды перпендикулярна её основанию, а две соседние с ней грани образуют с основанием двугранные углы по 30 градусов. Найдите площадь полной поверхности пирамиды, если её высота равна h.
Дано: пирамида PABCD ; основание ABCD - квадрат
(APB) ⊥ (ABCD) ; (APD) ^(ABCD) = (BPC) ^(ABCD) =30°
PM ⊥(ABCD) ( M -основание иысоты)
PM = h
S пол - ?
Обозначаем AB = BC = CD =DA = a
AD ⊥ AM ⇒ AD ⊥AP (теореме 3-х перпендикуляров)
∠PAM =30° линейный угол двугранного угла PADC
анологично :
∠PBM =30° линейный угол двугранного угла PBCD
→ BC ⊥ BM ⇒ BC ⊥BP (теореме 3-х перпендикуляров)
ΔPAM = ΔPBM (общий катет PM и ∠PAM =∠PBM= 30° острый угол)
⇒PA =PB ; Прямоугольные Δ PAD = Δ PBC (по двум катетам)
из ΔAMP: PM = AP/2 (как катет леж. против угла 30°)
AP =2*PM =2h и AM =√3 h . a = AB =2*AM =2√3 h .
PD =√(AP² +AD²) =√( (2h)² + (2√3 h)² ) = √ (4h² + 12h²) =√16h² =4h
PN =√(PD² - DN²) =√(PD² - AM²) = √ (16h² - 3h²) =√13 h
S пол =Sосн + S бок = S(ABCD) + [S(APB) +S(APD)+ S(BPC) +S(DPC) ] =
= S(ABCD) +S(APB) +2S(APD)+ S(DPC) =
a² +(1/2)*AB*PM + 2S(APD) +(1/2)*DC*PN =
= a² +(1/2)*a*h + 2a*PA/2+(1/2)*a*PN = || a =2√3h , PA =2h , PN =√13 h || =
=(2√3 h)² +√3 h² +2√3 h*2h +√3*√13 h² =( 12 +5√3 +√39) h²
ответ: S пол = ( 12 +5√3 +√39) h² .
Держи✔️
y=5x² - 48x + 91
а) координаты вершины параболы y=ax²+bx+c
В(х;у)
х(в) = -b/2a
x(B) = 48 / 10 = 4.8
y(B) = 5*4.8² - 48*4.8 + 91=115.2-23.04+91=183.16
B(4.8; 183.16)
b) направление ветвей параболы
ветви вверх, так как a>0
c) уравнение оси симметрии
х=4,8
d) координаты точек пересечения с осями Oх; Оу
у=0 (х; 0)
5x² - 48x + 91=0
Д= 2304 - 4*5*91 = 484=22²> 0 , значит, 2 корня
х(1) = (48+22)/10=7
х(2) = (48-22)/10 =2,6
(7;0) и (2,6; 0) - точки пересечения с осью х
х=0 (0; у)
у =5x² - 48x + 91
у=91
(0; 91) - точка пересечения с осью у
Подробнее - на -
Задача 6
В ΔАВС , АВ=ВС, АЕ -биссектриса, Е∈ВС. Найти Р( АВС), если ВС-АС=8 и ВЕ:ЕС=3:2.
Решение.
Пусть одна часть х. Тогда ВЕ=3х, ЕС=2х ⇒ ВС=5х ⇒ АВ=5х , т.к треугольник равнобедренный.
По т. о биссектрисе треугольника
, тогда 
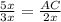⇒ AC=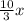
.
По условию ВС-АС=8 , поэтому 5х-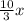
= 8 или 
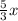=8 или х=4,8.
ВС=5*4,8=24 , АВ=24 , АС=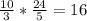
.
Р=24+24+16=64.
Задача 8
Стороны треугольника относятся как 2:3:3 . Найти периметр треугольника , если основание на 5 единиц меньше боковой стороны.
Решение .
Дан ΔАВС. АВ=ВС . Пусть одна часть х. Тогда АВ=ВС=3х, АС=2х .
По условию АС меньше АВ на 5, т.е АВ-АС=5.
Получим 3х-2х=5 или х=5 . Тогда АВ=ВС=3*5=15, АС=2*5=10 .
Р=15+15+10=40.
Задача 9
Угол при вершине равнобедренного треугольника равен 120°. , высота , опущенная на основание, равна 6 .Найти периметр треугольника .
Решение .
Дан ΔАВС , АВ=ВС ,ВН⊥АС , ∠АВС=120°.
1) Высота равнобедренного треугольника является биссектрисой ⇒∠АВН=60° .
2) ΔАВН -прямоугольный , по свойству углов ∠А=90°-60°=30°.
Против угла в 30° , лежит катет равный половине гипотенузы , т.е ВН=1/2*АВ ⇒ АВ=12 ⇒ВС=12, т.к треугольник равнобедренный.
По т. Пифагора АН²=АВ²-ВН² или АН²=12²-6² или АН=√18*6=6√3.
3) Высота равнобедренного ΔАВС является медианой, значит АН=НС=6√3 ⇒АС =12√3.
4)Р=12√3+12+12=24+12√3.