обозначим проекции точек а; в; с; d и точки о - точки пересечения диагоналей :
a_(1); b_(1); c_(1); d_(1); o_(1)
рассмотрим прямоугольные трапеции aa_(1)d_(1)d и вв_(1)с_(1)с
пересекаются по прямой оо_(1)
оо_(1)- средняя линия трапеции aa_(1)d_(1)d
оо_(1)- средняя линия трапеции вв_(1)с_(1)с
так как средняя линия трапеции равна полусумме оснований, то
из трапеции aa_(1)d_(1)d:
оо_(1)=(аа_(1)+dd_(1))/2
из трапеции вв_(1)с_(1)с :
оо_(1)=(bb_(1)+cc_(1))/2
приравниваем правые части:
(аа_(1)+dd_(1))/2=(bb_(1)+cc_(1))/2 ⇒ [b]аа_(1)+dd_(1)=bb_(1)+cc_(1)[/b]
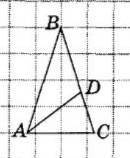
< В=36 град
АВ=ВС - по условию
Значит, тр-к АВС - равнобедренный
Значит, углы при основании равны :
< А=<С = (180-36):2= 72 град
Рассмотрим тр-к АВД :
< В=36 град - по условию
< ВАД=< ДАС= 72:2=36 град , т к АД- биссектриса
Рассмотрим тр-кмАДС :
< ДАС=36 град
< АСД=72 град
< АДС= 180-(36+72)
< АДС= 72 град
Углы при основании равны , значит, тр-к АДС - равнобедренный