Объяснение:
У ромба все стороны равны.
ΔMNP - равносторонний (все углы по 60°). Значит сторона ромба равна 30 см, а периметр Р=4*30=120 см.
***
2. Пусть меньшая сторона равна х см. Тогда большая будет х+5.
2(х+х+5)=66;
2х+5=33;
2х=28;
х=14 см - меньшая сторона.
х+5=14+5=19 см - большая сторона.
Проверим:
Р=2(14+19)=2*33=66 см. Все верно.
***
3. Диагонали прямоугольника в точке пересечения делятся пополам. АО=ОС=ОD=24/2=12 см.
РAOD=AO+OD+AD=12+12+16= 40 см.
***
4. Диагонали в ромбе являются и биссектрисами.
Если ∠ВАС=18°, то ∠А=18°*2=36°.
∠А=∠С=36°.
∠В=180°-(∠ВАС+∠ВСА)=180°-(18°+18°)=180°-36°=144°;
∠В=∠D=144°.
***
5. Пусть АК=4х. Тогда KD=2х.
4х+2х=12;
6х=12;
х=2;
АК=4*2=8 см;
KD=2*2=4 см.
∠ABK=∠KBC=180°/3=60° - ( равны смежному углу с углом В.)
Значит ΔАВК - равносторонний: АВ=ВК=AK=СD=4 см.
Р=2(АВ+ВС)=2(4+12) =2*16=32 см.
S бічної поверхні = 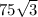 сантиметрів квадратних
сантиметрів квадратних
Объяснение:
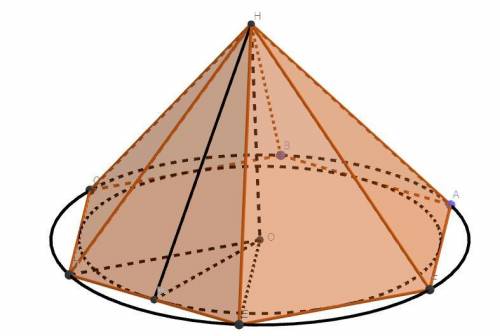
Дано: Правильна шестикутна піраміда, R = 5 см, α = 30°(α - бічні грані правильної шестикутної піраміди нахилені до основи під кутом α)
Знайти:
S - ?(площу бічної поверхні)
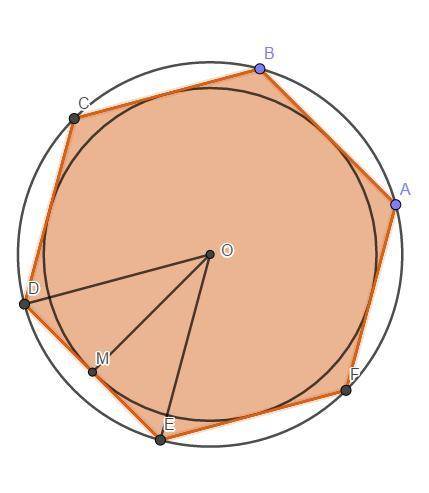
Розв'язання: Розглянемо правильний шестикутник ABCDEF. Проведемо відрізки OD і OE і розглянемо трикутник Δ DOE, який буде рівнобедренним тому, що OD = OE (OD = OE = 5см за умовою), як радіуси описаного кола.Позначимо середину відрізка DE у точці M і з вершини O проведемо відрізок OM - який буде медіаною. За умовою ∠HMO = α.За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, а так як OM⊥DE, то OM є радіусом вписаного кола.У правильного шестикутника 6 сторін, а отже шість центральних кутів, нехай центральний кут β, тоді ∠DOE = β, усі 6 центральних кутів утворють повне коло отже ∠DOE = β = 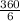 = 60°.
= 60°.
Так як OM - бісектриса за властивістю рівнобедренного трикутника, то
∠DOM = ∠MOE = ∠DOE : 2 = 60° : 2 = 30°.OM є висотою, тоді
sin ∠MOE = 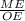 ⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.
⇒ ME = OE * sin ∠MOE = 5 * 0,5 = 2,5 см.Так як за OM - медіана, то DE = 2DM = 2ME = 2 * 2,5 = 5 см.
cos ∠MOE =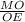 ⇒ MO = cos ∠MOE * OE = cos 30° * OE =
⇒ MO = cos ∠MOE * OE = cos 30° * OE = 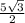 =
= 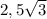
Проведемо відрізок OH - який буде висотою за властивісью шестикутної піраміди.РозглянемоΔ MOH.
cos ∠MOH = cos α = 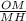 ⇒ MH =
⇒ MH = 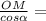
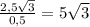 .
.
За властивістю правильної піраміди усі її грані є рівними рівнобедренними трикутниками, отже Δ HDE - рівнобедренний.Проведемо відрізок HM - який є медіаною так як DM = ME, За властивістю рівнобедренного трикутника медіана проведена до основи є бісектрисою і висотою, отже 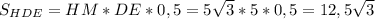 .
.
S бічної поверхні = 6 * 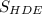 =
= 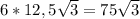 .
.
решение на фотографии.