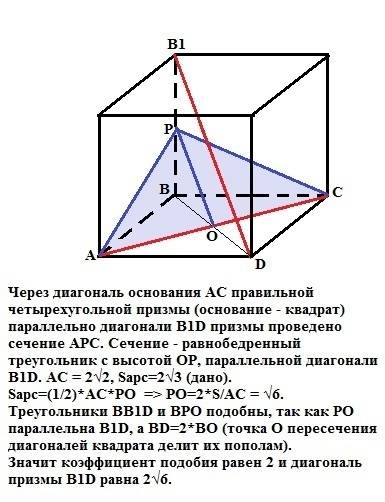
Через диагональ основания АС правильной четырехугольной призмы (основание - квадрат) параллельно диагонали B1D призмы проведено сечение АРС. Сечение - равнобедренный треугольник с высотой ОР, параллельной диагонали B1D. АС = 2√2, Sapc=2√3 (дано).
Sapc=(1/2)*AC*PO => PO=2*S/AC = √6. Треугольники BB1D и BPO подобны, так как РО параллельна B1D, а BD=2*ВО (точка О пересечения диагоналей квадрата делит их пополам). Значит коэффициент подобия итреугольников равен 2 и диагональ призмы B1D равна РО*2 = 2√6.
ответ: диагональ призмы равна 2√6.
А1А2 = А2А4 и <А2А1А4 = 45град ><А1А4А2 = 45град, <А1А2А4 = 90град
А1А4 = А2А3 = 8,8дм
По теореме Пифагора А1А2^2 + A2A4^2 = A1A4^2
2A1A2^2 = 8.8^2
A1A2 = 8.8 / V2
Sпар = 2*S( треуг.А1А2А4) = 2*1/2 *А1А2*А2А4 = (8,8/V2)*(8.8/V2) = 38.72(дм^2)