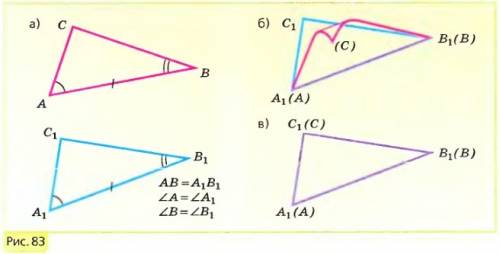
Доказательство. Рассмотрим треугольники ABC и A1B1C1, у которых AB = A1B1, ∠A = ∠A1, ∠B = ∠B1 (рис. 83, а), и докажем, что эти треугольники равны.
Мысленно наложим треугольник ABC так, чтобы вершина A совместилась с вершиной A1, сторона AB – с равной ей стороной A1B1, а вершина C и C1 оказались по одну сторону от прямой A1B1 (рис. 83, б).
Так как ∠A = ∠A1 и ∠B = ∠B1, то сторона AC наложится на луч A1C1, а сторона BC – на луч B1C1. Поэтому вершина C – общая точка сторон AC и BC – совместится с общей точкой лучей A1C1 и B1C1, т. е. с точкой C1 (рис. 83, в). Из этого следует, что стороны AC и BC совместятся соответственно со сторонами A1C1 и B1C1. Итак, треугольники полностью совместятся, и, следовательно, они равны. Теорема доказана.
Т.к по условию KM и AE диаметры ,то OK=AO=MO=EO(как радиусы),а углы AOK и MOE равны(как вертикальные)=> Треугольники AOK и MOE равны по двум сторонам и углу между ними=>AK=ME
Теперь докажем,что треугольники AOM и KOE равны. Углы AOM и KOE равны(как вертикальные),а ОКЕ=АМО и МАО=ОЕК(как накрест лежащие )=>треугольник АОМ равен треугольнику КОЕ по трём углам=>КЕ=АМ,а угол МКЕ равен углу АМК как накрест лежащие
Если не нравится доказательство в начале,то можно доказать аналогично тому,что во второй