Чертежи во вложениях.
1) По свойству отрезков касательных, проведенных к окружности из одной точки:
ВК=ВР=8, АР=АМ=12. СМ=СК=х.
По теореме Пифагора в ∆АВС АВ²=АС²+ВС²
20²=(12+х)²+(8+х)²
2х²+40х-192=0
х=-24 - не удовлетворяет условию
х=4
АС=12+4=16, ВС=8+4=12
S∆=1/2*FAC*BC=1/2*16*12=96
ответ:96.
2) Проведем высоты ВМ и СК, ВМ⊥АД и СК⊥АД.
Т.к. трапеция равнобедренная, то углы при большем основании равны, углы при меньшем основании тоже равны.
∆АВМ=∆СКД по гипотенузе и острому углу. Значит, АМ=КД=(АД-ВС):2=(18-10):2=4
В прямоугольном ∆АВМ ВМ=АМtg60°=4√3.
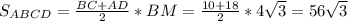

Решение будет в приложенном рисунке.