Смотри рисунок, там r- радиус
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение:
Площадь S1 боковой поверхности призмы равна произведению периметра перпендикулярного сечения призмы на её боковое ребро. Плоскость перпендикулярного сечения пересекает боковые грани по их высотам. Поэтому периметр перпендикулярного сечения равен сумме этих высот, т. е. 3*2=6.
Значит, S1 = 3al = 18
ПустьS -- площадь основания призмы. Площадь ортогональной проекции основания призмы на плоскость, перпендикулярную боковым рёбрам, равна площади перпендикулярного сечения, делённой на косинус угла между плоскостями основания и перпендикулярного сечения. Этот угол равен углу между боковым ребром и высотой призмы, т. е. 60∘.
Поэтому
S2= 2√3Следовательно, площадь полной поверхности призмы равна
Вывожу :
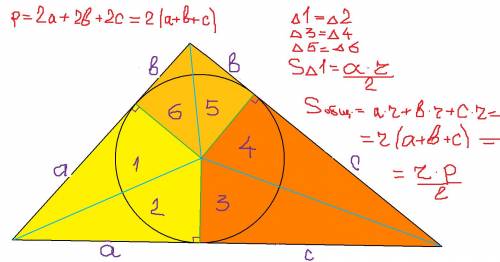
Треугольник АВС, стороны AB = c, AC = b, BC = a; r - радиус вписанной окружности.
Соединяю центр вписанной окружности с вершинами. Треугольник АВС "разрезан" на 3 треугольника - АОВ, АОС и ВОС. В треугольнике АОВ из точки О опускаю перпендикуляр на АВ. Он попадает в точку касания и по длине равен r. Поэтому площадь АОВ равна c*r/2; аналогично площадь треугольника ВОС равна a*r/2, площадь треугольника АОС равна b*r/2. Складываем эти площади, получаем площадь АВС.
S = (a + b + c)*r/2;
чтд