см. рис во вложении
Находим радиус вписанной окружности
r=√((p-a)(p-b)(p-c)/p)
p-полупериметр
p=(13+14+15)/2=21
r=√((21-15)(21-14)(21-13)/21)=4
Из треугольника OMB находим BM
BM^2=5^2-4^2=25-16=9
BM=3
Вся хорда 2ВМ=6
ответ 6
Дано:
тр АВС (уг С=90)
АС = 16 см
ВС = 12 см
АВ = 20 см
Найти:
а) косинус меньшего угла
б) сумму квадратов косинусов острых углов
а) по свойству соотношения сторон и углов треугольника, против меньшей стороны лежит меньший угол, а значит меньшим будет угол, лежащий против стороны 12 см, по условию, следовательно, это угол А.
cos A = AC / AB; cos A = 4/5 = 0.8
б) Есть св-во - оно же основное геометрическое тождество, сумма квадратов косинусов острых углов прямоугольного треугольника равна единице, но вы похоже этого ещё не изучали, посему надо найти оставшийся косинус угла В и найти сумму квадратов косинусов вычислением, приступим:
cos B = CB / AB; cos B = 12/20 = 3/5 = 0.6
cos²A +cos²B = 0.8²+0.6²=0.64+0.36=1
Поиск...
3
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
Ruvioo
26.01.2015
Геометрия
5 - 9 классы
ответ дан • проверенный экспертом
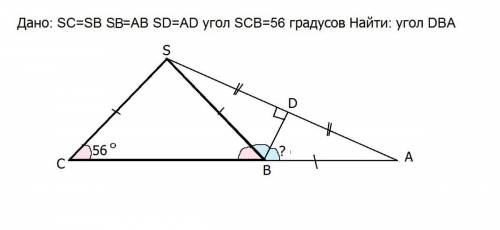
! Дано: SC=SB Sb=AB SD=AD угол SCB=56 градусов Найти: угол DBA
1
СМОТРЕТЬ ОТВЕТ
ответ, проверенный экспертом
3,0/5
19
Hrisula
главный мозг
7.7 тыс. ответов
83.3 млн пользователей, получивших
Треугольник SCB - равнобедренный по условию.
Углы при основании СВ равны. Угол SBC =SCB=56°
Угол SBA cмежный и равен 180°- 56°=124°
В треугольнике SBA по условию SB=BA, он тоже равнобедренный.
SD=DA, следовательно, ВD - медиана.
В равнобедренном треугольнике медиана является биссектрисой и высотой.
ВD - биссектриса,⇒ угол АBD - половина угла SBA и равен 124°:2=62°
Можно найти и угол DSB
Треугольник SDB- прямоугольный, т.к. ВD - высота.
Угол DSB равен 90°-62°=28°
Если радиус окружности R, расстояние до хорды r, длина хорды m, то
(m/2)^2 + r^2 = R^2;
Поскольку центр окружности совпадает с центром вписанной в треугольник окружности, расстояние до искомых хорд будет одинаковым - равным радиусу вписанной окружности. То есть r - это радиус вписанной окружности в треугольник со сторонами 13,14,15.
ПОЛУпериметр этого треугольника равен (13 + 14 + 15)/3 = 21;
Площадь треугольника легко считается по формуле Герона и равна 84.
Этот треугольник составлен из двух Пифагоровых треугольников - со сторонами (9,12,15) и (5,12,13), приставленных друг к другу катетами 12 так, что катеты 9 и 5 вместе образуют сторону 14. Поэтому высота к стороне 14 равна 12, а площадь 12*14/2 = 84.
r = S/p = 84/21 = 4;
откуда
m/2 = 3; (здесь тоже Пифагорова тройка 3,4,5, самая первая)
m = 6; (все хорды одинаковые, само собой)