В треугольнике ABC отмечены точки D на AB и E на AC так, что ADE= CBA AE=8 DE=10 BC=30, а BD на 15 больше - id1727039020200623 от karinatom9 23.06.2020 08:09

Question

Геометрия: В треугольнике ABC отмечены точки D на AB и E на AC так, что ADE= CBA AE=8 DE=10 BC=30, а BD на 15 больше чем AD. Найди AB AC очень ​

karinatom9 · Accepted Answer

Да, треугольники будут равны.

Решение

Пусть BM и B1M1 – медианы треугольников ABC и A1B1C1, AB = A1B1, BM = B1M1, BC = B1C1.

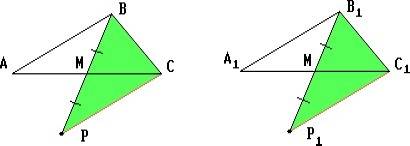
Отложим на продолжениях медиан BM и B1M1 за точки M и M1 отрезки MP и M1P1, равные соответственно BM и B1M1 Тогда из равенства треугольников PMC и BMA следует, что PC = AB, а из равенства треугольников P1M1C1 и B1M1A1 – что P1C1 = A1B1. Поэтому треугольники PBC и P1B1C1 равны.

Следовательно, ∠MBC = ∠M1B1C1. Значит, треугольники MBC и M1B1C1 равны. Поэтому MC = M1C1 и AC = A1C1. Следовательно, треугольники ABC и A1B1C1 равны по трём сторонам.

Будут ли равны треугольники , соответственно по двум сторонам и медиане , исходящим из одной вершины

В треугольнике ABC отмечены точки D на AB и E на AC так, что ADE= CBA AE=8 DE=10 BC=30, а BD на 15 больше чем AD. Найди AB AC очень ​

MOGZ ответил

В треугольнике ABC отмечены точки D на AB и E на AC так, что ADE= CBA AE=8 DE=10 BC=30, а BD на 15 больше чем AD. Найди AB AC очень