Диагонали ромба точкой пересечения делятся пополам (как и у параллелограмма)
Диагонали ромба взаимно перпендикулярны
Диагонали ромба являются биссектрисами его углов
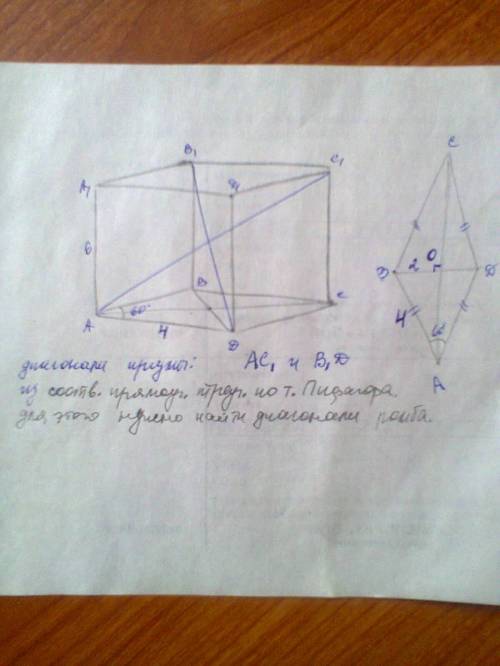
из треуг.BOA: угол BAO=30, катет BO = 4/2 = 2 (катет против угла в 30 град.=половине гипотенузы) и по т.Пифагора второй катет = корень(4^2-2^2) = 2корень(3)
следовательно, диагонали ромба равны
BD = 2BO = 4
AC = 2AO = 4корень(3)
AC1^2 = AC^2 + CC1^2 = 4*4*3 + 6*6 = 4*(12+9) = 4*21
AC1 = 2корень(21)
B1D^2 = BD^2 + CC1^2 = 4+36 = 40
B1D = 2корень(10)
Согласно теории площадь круга зависит от радиуса этого круга и связана с радиусом формулой S=π·r². Следовательно, часть круга также хависит от радиуса этого круга.
По сему, непонятно, по какой причине автор не указал явно или неявно на радиус.
Пусть r-радиус круга, тогда в ∆АВС сторона АВ=2r.
Проведем еще один радиус ОК. Тогда требуемая площадь может быть найдена как сумма площади ∆АОК и площади сектора КОВ.
∆ОАК - равнобедренный с основанием АК, тогда ∠АОК=180°-(30°+30°)=120°.
S ∆АОК = ½ OA·OK·sin∠АОК= ½ r²·sin120°= ½ r²·sin60°= (r²·√3)/4.
∠ВОК и ∠АОК - смежные.
∠ВОК=180°-120°=60°
Площадь сектора КОВ:
Итак, площадь части круга, лежащей внутри треугольника, есть
Автору останется выяснить, чему равен радиус r круга, и поставить в последнее выражение.