Объяснение:
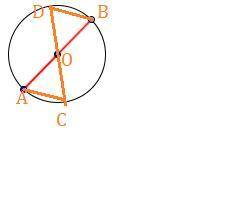
1)Дано окр. О(r) , АВ, СD-диаметры .
Доказать АС=BD
Доказательство.ΔАОС=ΔВОD по двум сторонам и углу между ними : АО=ОВ и СО=ОD как радиусы одной окружности, ∠АОС=∠ВОD как вертикальные .
2) Дано окр. О(r) , r=9 см , АВ, АС-касательные, ∠ВАС=120°.
Найти: АВ , АС.
Решение. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания ⇒∠ОВА=∠ОСА=90°. Проведем АО.
Отрезки касательных к окружности, проведенных из одной точки, равны , т.е АВ=АС , и составляют равные углы с прямой, проходящей через эту точку и центр окружности, т.е. ∠ВАО=∠САО=120°:2=60°.
ΔВАО : ∠ВОА=90°-60°=30°. Пусть АВ=х , по св. угла 30° ⇒ОА=2х. По т. Пифагора (2х)²=х²+9² или 3х²=81 или х²=27 или х=3√3. АВ=АС=3√3 см

416 см²
Объяснение:
Дано: КМРТ - трапеция, МК⊥КТ, МК=16 см, РТ=20 см. МТ - биссектриса. Найти S(КМРТ).
∠КТМ=∠РТМ по определению биссектрисы
∠РМТ=∠МТК как внутренние накрест лежащие при МР║КТ и секущей МТ, значит ΔМРТ - равнобедренный, МР=РТ=20 см.
Проведем высоту РН=МК=16 см.
КН=МР=20 см.
ΔРТН - прямоугольный, РТ=20 см, РН=16 см, значит ТН=12 см (египетский треугольник).
КТ=КН+ТН=20+12=32 см.
S=(МР+КТ):2*РН=(20+32):2*16=416 см²