
ответ: 5 (метров)
Объяснение: Обозначим высоту дома АВ, высоту фонаря МЕ, расстояние между домом и фонарем АМ ( см. рисунок), место, где лежат зерна, обозначим С.
Т.к. и дом, и фонарь перпендикулярны земле, соединив точки В и Е с точкой С, получим прямоугольные треугольники АВС и СЕМ, гипотенузы которых равны (так как голуби летели с равными скоростями и прилетели одновременно к зерну).⇒ ВС=СЕ
Примем АС=х, тогда СМ=17-х.
ВС²=ВА²+АС²
ЕС²=СМ²+ЕМ²
ВА²+АС²=СМ²+ЕМ²
12²+х²=(17-х)²+5², ⇒ 34х=170, х=5 (метров) = расстояние от дома до зерна.

ответ: 5 (метров)
Объяснение: Обозначим высоту дома АВ, высоту фонаря МЕ, расстояние между домом и фонарем АМ ( см. рисунок), место, где лежат зерна, обозначим С.
Т.к. и дом, и фонарь перпендикулярны земле, соединив точки В и Е с точкой С, получим прямоугольные треугольники АВС и СЕМ, гипотенузы которых равны (так как голуби летели с равными скоростями и прилетели одновременно к зерну).⇒ ВС=СЕ
Примем АС=х, тогда СМ=17-х.
ВС²=ВА²+АС²
ЕС²=СМ²+ЕМ²
ВА²+АС²=СМ²+ЕМ²
12²+х²=(17-х)²+5², ⇒ 34х=170, х=5 (метров) = расстояние от дома до зерна.

Найдите периметр треугольника с площадью 10√3 см² и углом 60°, если стороны, прилежащие к данному углу, относятся как 5:8.
Объяснение:
Пусть в ΔАВС , ∠В=60° , АВ:ВС=5:8.
Если одна часть х см , то АВ=5х, ВС=8х.
S( треуг.) = 1/2*АВ*ВС*sinВ или 10√3=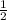 *5х*8х*
*5х*8х*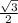 , х²=1 , х=1 ⇒
, х²=1 , х=1 ⇒
АВ=5 см , ВС=8 см .
По т. косинусов АС²=АВ²+ВС²-2*АВ*ВС*cosВ,
АС²=25+64-2*5*8*cos60, АС²=89-2*5*8*1/2, АС=7 см
Р=5+8+7=20 ( см)
====================
S( треуг.) = 1/2*а*в* sinα
Т. косинусов "Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними"