∠А=360°-99°-90°-90°=81°- находим как разность 360°- это сумма углов выпуклого четырехугольника, 99°- угол, вертикальный углу СОВ, и двух прямых углов от высот проведенных на две стороны АВ и АС треугольника АВС. Если точка пересечения АВ с высотой, ПРОВЕДЕННОЙ ИЗ вершины С, есть точка С₁, точка пересечения АС с высотой, ПРОВЕДЕННОЙ ИЗ вершины В, есть точка В₁, то выпуклый четырехугольник, о котором речь в решении - это АС₁ОВ₁, вот из него и находим интересующий нас угол А.
Только не просите рисовать треугольник. Это просто. А у меня нет такой возможности.
ответ 81⁰
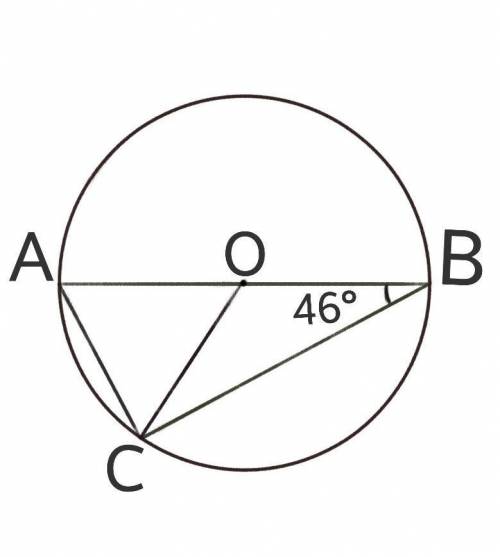
1) Розглянемо трикутник ВОС:
ОВ = ОС = R (радіуси) => трикутник BOC - рівнобедрений => кут АВС = кут ОСВ = 46° => кут СОВ = 180° - (кут АВС + кут ОСВ) = 180° - (46° + 46°) = 180° - 92° = 88° (за теоремою про суму кутів трикутника)
2) Розглянемо трикутник АОС:
кут АОС = 180° - кут СОВ = 180° - 88° = 92° (як суміжні кути)
ОА = ОС = R (радіуси) => трикутник АОС - рівнобедрений => кут ОАС = кут АСО
Нехай кут ОАС = кут АСО = х
За теоремою про суму кутів трикутника маємо рівняння:
х + х + 92° = 180°
2х = 88° /:2
х = 44°
Відповідь: кут АСО = 44°
(У ФАЙЛІ ПРИКРІПИВ МАЛЮНОК ДО ЗАДАЧІ)
Пусть площадь АВС s = 48;
Площадь треугольника ALC равна S/4, поскольку LC/BC = 1/4, а высоты у ABC и ALC - общие - это расстояние от А до ВС. При этом расстояние от М до ВС составляет 3/4 расстояния от А до ВС (оставляю доказательство этого элементарного утверждения вам, подсказка - надо провести перпендикуляры к ВС из А - АН и из М - МР и рассмотреть подобные треугольники AHC и MРC, причем МС/АС = 3/4), поэтому площадь треугольника MLC равна (S/4)*(3/4) = 3*S/16;
Точно так же площади треугольников АМК и BKL равны 3*S/16;
Поэтому площадь треугольника MLK равна S - 3*(3*S/16) = 7*S/16 = 21;