с геометрией 5. 3 точки М плоскости & проведено перпендикуляр МО и наклонные МА и МВ, которые образуют с перпендикуляром углы 60 ° i 45 ° соответственно. Найти расстояние между основаниями наклонных, если наклонные взаимно перпендикулярны, а длина перпендикулярна равна √3 см.
6. Через вершину А треугольника АМD, у которого АМ=AD =5 см, MD=6 см к его плоскости проведен перпендикуляр АK=4√3см. Найти расстояние от точки К к стороне MD.
-------------------
см приложение
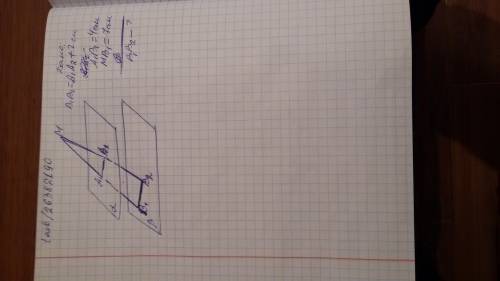
α || β ;
B₁B₂ = A₁A₂ + 2 ;
MB₁ = 7 см ;
A₁B₁ =4 см .
--------------
B₁B₂ =x → ?
Так как плоскости α и β параллельны , то будут параллельны и линии пересечении плоскости B₁MB₂ (≡пл A₁MA₂ ) с этими
плоскостями . А отрезки A₁A₂ и B₁B₂ лежать на эти линии , следовательно A₁A₂ || B₁B₂ .
---
ΔA₁MA₂ ~ ΔB₁MB₂ ;
A₁A₂ / B₁B₂ =MA₁ / MB₁ ;
(B₁B₂ -2) / B₁B₂ =( MB₁ -A₁B₁) / MB₁ ;
1 - 2 / B₁B₂ = 1 - 4 /7 ;
2 / B₁B₂ = 4 /7 ;
B₁B₂= 3,5 ( см ) .
ответ : 3,5 см .