Так как ΔABC — равносторонний, то: 
Это очень важно учитывать!
Стороны вписанного треугольника — перпеникулярны сторонам исходного треугольника ABC, то есть:
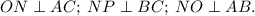
То есть, образуются прямоугольные треугольники: 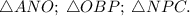
И так как углы исходного треугольника равны 60°, то:
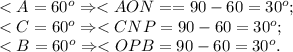
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов — равен половине гипотенузы.
То есть:
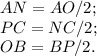
Также, эти прямоугольные треугольники друг другу равны, по двум углам (60°; 30°), и по одному катету: OP ≡ NO ≡ NP, так как вписанный треугольник — равносторонний.
И так как: 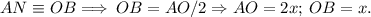
Вывод: Вершины вписанного треугольника делят сторону исходного треугольника в отношении: 2:1.
Дано: прямая а, точка А, принадлежащая прямой.
1) Проведем окружность произвольного радиуса с центром в точке А. Точки пересечения окружности с прямой а обозначим В и С.
2) Проведем две окружности одинакового произвольного радиуса (большего половины отрезка ВС), с центрами в точках В и С.
3) Через точки пересечения этих окружностей (К и Н) проведем прямую b.
Прямая b - искомый перпендикуляр к прямой а.
Доказательство:
А - середина отрезка ВС по построению (АВ = АС как радиусы одной окружности). Тогда КА - медиана треугольника ВКС.
Треугольник ВКС равнобедренный, так как ВК = СК как равные радиусы. Значит медиана КА является и высотой, т.е. КА⊥а.