Чертежи во вложении.
№1. Скорее всего автор совершил описку, и условие читать надо так: "Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2:1, считая от вершины острого угла."
Пусть ВМ-биссектриса тупого угла, пересекающая сторону АД в точке М, тогда АМ:МД=2:1.
Т.к. ∠1=∠2 (определение биссектрисы угла) и ∠2=∠3 (накрестлежащие при АД||ВС и секущей ВМ), то ∠1=∠3. Тогда ∆АВМ-равнобедренный с основанием ВМ, боковые стороны АМ=АВ.
Пусть МД=х, тогда АМ=АВ=2х, СД=АВ=2х, АД=ВС=3х.
Периметр параллелограмма Р=(АВ+ВД)*2. Получим уравнение:
2(2х+3х)=60
5х=30
х=6
Значит, МД=6.
АВ=2*6=12 - меньшая сторона параллелограмма.
ответ: 12.
№2. Объем пирамиды V=⅓·Sосн·H.
1) Проанализируем основание пирамиды -трапецию АВСД. Т.к. АВ=СД=1, то АВСД-равнобедренная. Проведем высоты ВН и СТ.
Sосн=½·(ВС+АД)·ВН.
ВС=НТ=1, АН+ТД=2-1=1.
Из равенства пямоугольных ∆АВН и ∆СТД следует, что АН=ТД=1/2=0,5.
Таким образом в прямоугольном ∆АВН гипотенуза АВ в 2 раза больше катета АН, значит, ∠АВН=30°, ∠ВАН=60°. Находим высоту ВН=АВ·cos30°=√3/2.
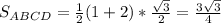
2) Определим куда проецируется вершина М пирамиды. Поскольку ребра пирамиды МА=МВ=МС=МД, то их проекции на полскость (АВСД) - это отрезки ОА=ОВ=ОС=ОД. Значит, О-центр описанной окружности.
∠ВАД=60°, отсюда ⌣ВСД=120°.
Равенство хорд АВ, ВС и СД влечет за собой равенство дуг АВ, ВС и СД. Тогда ⌣ВС=⌣СД=120°:2=60°, а значит, и ⌣АВ=60°. Тогда ⌣АВСД=180° и АД-диаметр описанной около трапеции окружности. Тогда О лежит на диаметре АД. ОА=ОВ=ОС=ОД=½АД=1
Найдем высоту пирамиды МО из прямоугольного ∆МОД.
В равностороннем ∆АМД МО- медиана, биссектриса, высота. По теореме Пифагора
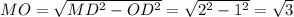
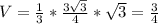
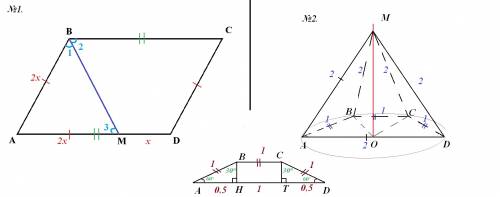
ответ: 3/4.
Объяснение:
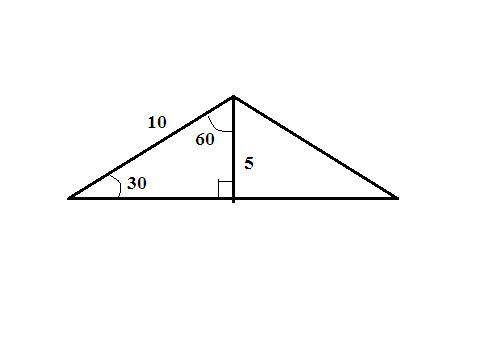
1. находим боковые стороны равнобедренного треугольника через его площадь:
S=a²sin120°/2 ⇒ a²=(25√3)/(√3/2)/2=25*4, a=√(25*4)=5*2=10 см - боковые стороны.
2. находим основание:
высота, проведенная к основанию равнобедренного треугольника, образует с боковой стороной и половиной основания прямоугольный треугольник где гипотенуза - боковая сторона - 10 см. Углы в этом треугольнике 90°, 60°, 30°. Против угла 30° (высота треугольника) лежит катет в два раза меньше гипотенузы ⇒ высота - 10/2=5 см;
далее либо по т. Пифагора находим половину основания треугольника, либо через формулу нахождения площади находим длину всего основания.
т. Пифагора: √(10²-5²)=√75=5√3 см - половина основания, (5√3)*2=10√3 - основание треугольника;
через площадь: в*h/2=25√3, в=50√3/5=10√3 см.
x + 3y + 3 = 0
Объяснение:
Стороны:
5x - y - 1 = 0
x - y - 9 = 0
Точка пересечения высот: H(1; -2).
Уравнение высоты, перпендикулярной к прямой 5x - y - 1 = 0:
h1 : (x - 1) + 5(y + 2) = 0; x + 5y + 9 = 0
Вершина, из которой выходит эта высота, есть точка пересечения высоты и стороны x - y - 9 = 0:
{ x + 5y + 9 = 0
{ x - y - 9 = 0
Решаем подстановкой:
{ y = x - 9
{ x + 5(x-9) + 9 = 0
6x - 36 = 0; x = 6; y = -3. A(6; -3).
Уравнение высоты, перпендикулярной к прямой x - y - 9 = 0:
h2 : (x - 1) + (y + 2) = 0; x + y + 1 = 0
Точно также находим точку пересечения высоты и стороны 5x - y - 1 = 0:
{ x + y + 1 = 0
{ 5x - y - 1 = 0
Решаем тоже подстановкой:
{ y = 5x - 1
{ x + 5x - 1 + 1 = 0
6x = 0; x = 0; y = -1. B(0; -1)
Теперь строим уравнение прямой по двум точкам:
(AB) : (x-6)/(0-6) = (y+3)/(-1+3)
(x-6)/(-6) = (y+3)/2
2(x-6) = -6(y+3)
2x - 12 = -6y - 18
2x + 6y + 6 = 0
x + 3y + 3 = 0
1)P=2(a+b) , где а и в стороны параллограмма
а=x+2x=3x следовательно другая сторона равна x так как равны углы .
2(x+3x)=60
4x=30
x=7.5см
а если от острого
2(3x+2x)=60
5x=30
x=6
ответ 6 см
2) вторую задачу вам решили