Формула для расчитывания объёма параллелепипеда: V = abc;
нам надо найти высоту.
1)Воспользуюсь пространственной теоремой Пифагора,
d² = a² + b² + c² откуда
с² = d² - a² - b² = 11² - 6² - 7² = 121 - 36 - 49 = 36
c = 6
2)V = abc = 6 * 7 * 6 = 36 * 7 = 252 см³
Сторона меньшего основания правильной треугольной усечённой пирамиды равна 2 см, а боковое ребро пирамиды, равное √2 см , образует со стороной большего основания угол 45° . Найдите полную поверхность пирамиды.
Объяснение:
S( полное)=S(в.осн.)+S(н.основ)+S(бок) ,
1) S(прав.треуг.)=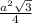
, S(в.осн.)=
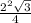=√3 (см²).
2)Боковые грани - равнобедренные трапеции . Пусть в трапеции
ВСС₁В₁ отрезки В₁Н, С₁К- высоты. Тогда ΔВВ₁Н-прямоугольный ,равнобедренный (∠ВВ₁Н=90°-45°=45°)⇒ВН=В₁Н=х. По т. Пифагора х²+х²=(√2)² ,х=1. Значит В₁Н=1 , ВС=ВН+НК+КС=1+2+1=4 (см).
3) S(н.осн.)=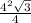
=4√3 (см²).
4)S(бок) =3*S(трапеции ВСС₁В₁) =3* 1/2*В₁Н*(ВС+В₁С₁)=3*1/2*1*6=9(см²).
5)S( полное)=√3 +4√3 +9=9+5√3 ( см²) .
18 см
Объяснение:
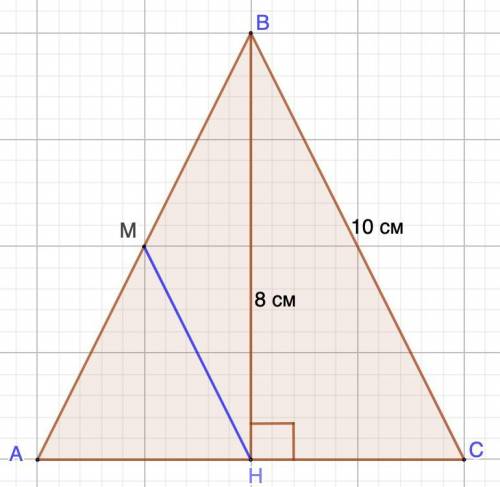
Дано: ΔАВС - равнобедренный.
ВС = 10 см;
ВН = 8 см - высота
BM || BC
Найти: Р (ΔВМН)
Рассмотрим ΔАВС - равнобедренный.
В равнобедренном треугольнике высота , проведенная к основанию, является медианой.⇒ АН = АС
НМ || ВС (условие)
Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.⇒ НМ - средняя линия.
⇒ АМ = МВ = 10 : 2 = 5 (см)
Средняя линия треугольника равна половине основания.⇒ НМ = ВС : 2 = 10 : 2 = 5 (см)
Периметр равен сумме длин всех сторон.Р (ΔВМН) = МВ + ВН + МН = 5 +8 +5 = 18 (см)
Формула объема: V = abc
квадрат диагонали = сумме квадратов все трех измерений.
11² = 6² + 7² + c²
121 - 36 - 49 = c²
c = 6
V = 6*7*6 = 252.