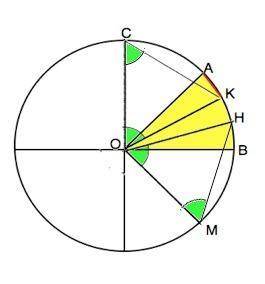
Дан угол АОВ=45°.
Из О как из центра чертим окружность произвольного радиуса. Проводим через О общепринятым перпендикулярно стороне ОВ прямую до пересечения с окружностью – диаметр.
Угол АОС=АОВ=45°.
Тем же радиусом из т. С делаем насечку в т. К на дуге АВ, т. К соединяем с т.О
Угол СОК=60° ( треугольник АОК - равносторонний)
Угол АОК=∠СОК-∠СОА=60°-45°=15°
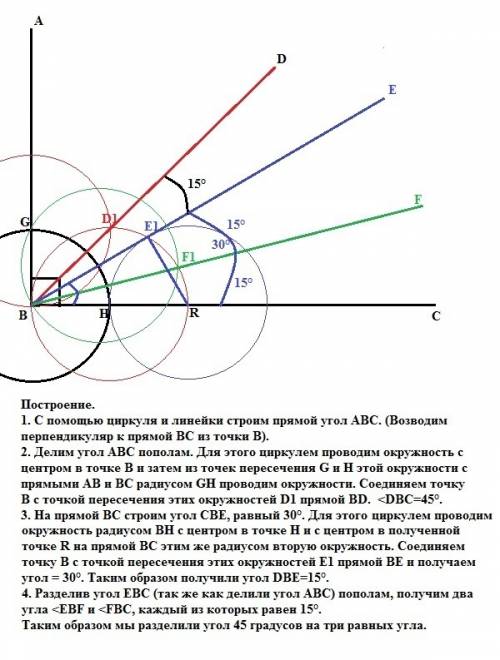
а) Проводим биссектрису ОН угла КОВ. Данный угол поделен на 3 равные части. Или:
б) раствором циркуля, равным хорде АК. от т. В отмечаем на дуге АВ точку Н и соединим ее с О.
АОК=КОН=НОВ=15°.
-----------
Как вариант можно отложить от ОВ угол ВОМ=45° и от т.М тем радиусом ОВ отметить на дуге АВ т.Н.
х = 3
Объяснение:
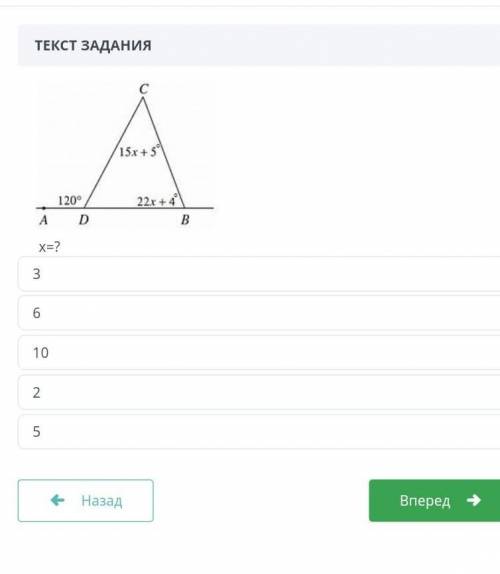
Сумма углов треугольника равна 180°. Поэтому решать надо уравнение, которое будет состоять из суммы всех углов. Угол С = 15х + 5, угол В = 22х + 4, а угол А= 180 - 120 = 60 (поскольку углы ADC и CDB - смежные, их сумма равна 180°
И вот, уравнение:
15х + 5 + 22х + 4 + 60 = 180
37х + 69 = 180
37х = 180 - 69
37х = 111
х = 111 : 37
х = 3