Так как у ромба диагонали пересекаются в точке О(назовёмеё так)⇒делятся пополам и пересекаются под прямым углом,углом 90 градусов.Половина диагонали BD=15см.По теореме Пифагора найдём АО:корень квадратный из 17^2-15^2=8-половина второй диагонали⇒вся диагональ=АО*2=8*2=16 см.
ответ:16 см.
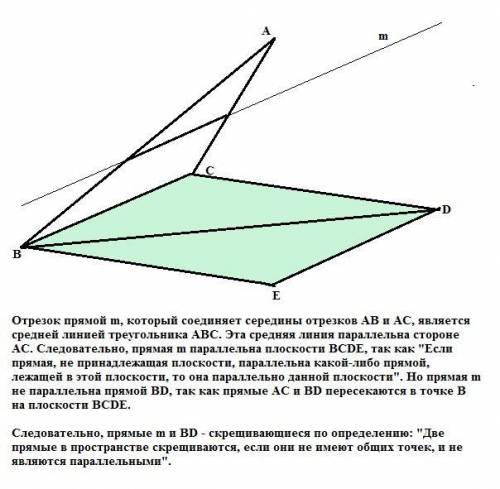
Прямые BD и m - скрещивающиеся прямые.
Объяснение:
Отрезок прямой m, который соединяет середины отрезков AB и AC, является средней линией треугольника АВС. Эта средняя линия параллельна стороне АС. Следовательно, прямая m параллельна плоскости ВСDE, так как "Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости". Но прямая m не параллельна прямой BD, так как прямые АС и BD пересекаются в точке В на плоскости BCDE.
Следовательно, прямые m и BD - скрещивающиеся по определению: "Две прямые в пространстве скрещиваются, если они не имеют общих точек, и не являются параллельными".

В ромбе диагонали в точке пересечения делятся пополам и пересекаются под прямым углом.Пусть АВ сторона ромба, О точка пересечения диагоналей.
АВ=17, BО=15 по т. Пифагора AО^2=17^2-15^2=(17-15)(17+15)=2*32=64
AO=8, AC=16