
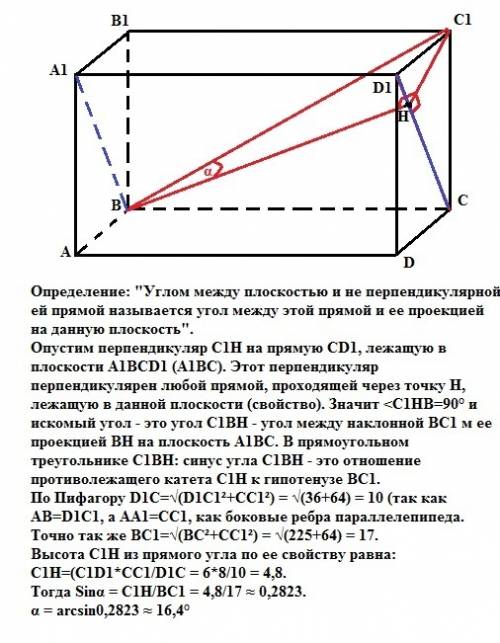
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
Основание правильной четырёхугольной пирамиды — квадрат, а боковые грани — равные равнобедренные треугольники.
Пирамида SАВСД: основание АВСД (АВ=ВС=СД=АД=3√2), боковые ребра SА=SВ=SС=SД=5. Вершина пирамиды S проектируется в точку О пересечения диагоналей основания (квадрата) АС и ВД, т.е. SO- это высота пирамиды.
Проведем апофему пирамиды SK - это высота боковой грани (равнобедренного ΔSАВ), она же и медиана, и биссектриса.
SК=√(SA²-AK²)=√(5²-(3√2/2)²)=√(25-4,5)=√20,5
Из прямоугольного ΔSKО:
SО=√(SК²-OK²)=√((√20,5)²-(3√2/2)²)=√20,5-4,5=√16=4
Площадь основания Sосн=АВ²=3√2²=18
Периметр основания Р=4АВ=4*3√2=12√2
Площадь боковой поверхности
Sбок=P*SK/2=12√2*√20,5 /2=6√41
Площадь полной поверхности
Sполн=Sбок+Sосн=6√41+18
Объем
V=Sосн*SO/3=18*4/3=24
Подробнее - на -
параллельны только а и b вот 180-42=138 градусов