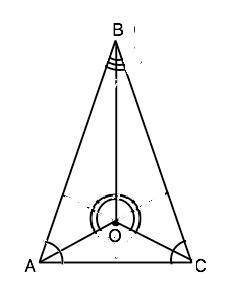
О - точка пересечения биссектрис треугольника АВС.
∠AOB = ∠COB. Найти наименьший угол треугольника ABC, если ∠ABC в три раза меньше ∠AOC
ответ: 36°
Объяснение:
ВО- биссектриса угла В, ∠AOB =∠COB (дано)⇒
∆ АОВ=∆ СОВ по двум углам при общей стороне ВО ( 2-й признак). ⇒
∠ВОА=∠ВОС.
Т.к. АО и СО - биссектрисы, то и ∠ВАС=∠ВСА. как состоящие из равных половинок. ⇒ ∆ АВС равнобедренный.
Примем ∠ОАС и ∠ОСА равными α. Тогда ∠АОС=180°-2α.
∠АВС=180°-4 α.
Составим уравнение согласно условию:
∠ АОС=3∠ АВС⇒
180°-2α=3(180°-4α). Произведя необходимые вычисления, получим 10α=360°⇒ α=36°
Угол АВС=180°-4•36°=36°.
Углы А и С вдвое больше α, они равны по 72°.
Следовательно, наименьший угол ∆ АВС - угол АВС=36°
Есил провести высоты из меньшего основания к большему, то эти высоты будут равны боковым сторонам трапеции (угол 45 градусов при основании+90 градусов при высоте позволяет сказать, что третий угол также равен 45 градусов, следовательно, треугольник получен равнобедренный). Отсюда получаем, что кусочки, отсечённые высотами меньшего основания равны самим высотам=5 см.
Находим большее основание:
6 (меньшее основание спроецировалось на большее с высот, т.е получился прямоугольник) см + 5 см + 5 см = 16 см.
ответ: 16 см.