Основание - прямоугольник, диагональ которого является диаметром цилиндра.
d = √6²+8²=√100=10 дм, R=d/2 = 5 дм
Осевое сечение цилиндра - прямоугольник с шириной d=10 и высотой h=14
S = 14*10 = 140 дм²
Поверхность параллелопипеда складывается из площадей оснований и площадей граней S=2ab+2ah+2bh=2*6*8+2*6*14+2*8*14=96+168+224 = 488 дм²
Поверхность цилиндра складывается из 2хоснований и боковой поверхности
S = 2πR² + 2πRh = 2π*25 + 2π*5*14 = 50π+140π=190π дм²
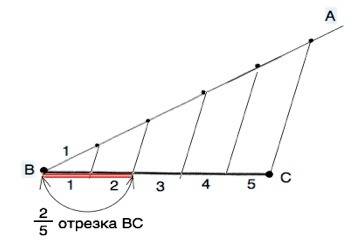
Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
использована теорема Пифагора, формула площади прямоугольника, площади полной поверхности цилиндра, площади полной поверхности параллелепипеда