1) Формула объёма конуса V=S•H:3=πr²H:3
Формула объёма шара
V=4πR³:3
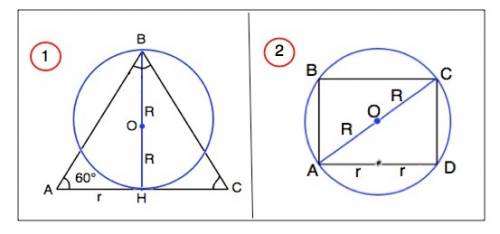
Осевое сечение данного конуса - равносторонний треугольник, т.к. его образующая составляет с плоскостью основания угол 60°.
Выразим радиус r конуса через радиус R шара.
r=2R:tg60°=2R/√3
V(кон)=π(2R/√3)²•2R²3=π8R³/9
V(шара)=4πR³/3
V(кон):V(шар)=[π8R³/9]:[4πR³/3]=(π•8R³•3/9)•4πR³=2/3
———————
2) Формула объёма цилиндра
V=πr²•H
Формула площади осевого сечения цилиндра
S=2r•H
Разделим одну формулу на другую:
(πr²•H):(2r•H)=πr/2⇒
96π:48=πr/2⇒
4π=πr
r=4
Из площади осевого сечения цилиндра:
Н=S:2r=48:8=6
На схематическом рисунке сферы с вписанным цилиндром
АВ- высота цилиндра, ВС - его диаметр,
АС - диаметр сферы.
АС=√(6²+8²)=√100=10
R=10:2=5
S(сф)=4πR8=4π•25=100π см²
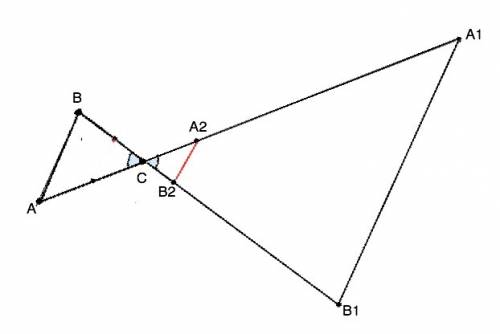
Обозначим данные точки А, В и С. Эти три точки можно соединить одним единственным в фигуру из трех точек и трех отрезков. Т.е. в треугольник , для которого предлагается построить два подобных с коэффициентом подобия k=3 и k=0,5 ( См. рисунки вложения)
Продлим ВС и АС и с циркуля 3 раза отложим длину этих сторон. Получим СА1=3АС и СВ1=3ВС. Угол А1СВ1 получившегося треугольника равен углу ВСА ( вертикальные). Треугольники АВС и А1В1С подобны по пропорциональным сторонам и равному углу между ними. Аналогично строится треугольник А2СВ2, подобный треугольника АВС с k=0,5. Для этого сначала делим две стороны пополам деления отрезка пополам циркулем Вы, конечно, уже знаете).
На сторонах угла ВАС от А циркулем на АС и АВ откладываем равные отрезки АМ и АК. Соединим М и К. На произвольной прямой отмечаем т.А1 и чертим окружность радиусом, равным АК. Точку пересечения с взятой прямой отмечаем К1. От К1 на окружности циркулем отмечаем точку М1 так, что К1М1=КМ. Из центра А1 окружности поводим прямую А1М1. Угол, равный углу ВАС исходного треугольника, построен. На прямых А1М1 и А1К1 откладываем стороны нужной длины: А1С1=3АС и А1В1=3 ВС и соединяем их. Аналогично для треугольника с k=0,5 откладываем половины длин сторон АС и АВ треугольника АВС и соединяем их. Стороны построенных треугольников пропорциональны сторонам исходного, а углы между ними равны углу ∆ АВС.

Даны координаты вершин треугольника АВС: А(-2;0), В(0;5), С(3;-2).
Составить уравнения:
а) стороны АС;
Вектор АС = (3-(-2); -2-0) = (5; -2).
Уравнение АС: (х + 2)/5 = у/(-2) каноническое.
2х + 5у + 4 = 0 общее.
у = (-2/5)х - (4/5) с угловым коэффициентом.
б) высоты ВD;
Так как ВД это высота (перпендикуляр) к АС, то коэффициенты А и В в общем уравнении меняются на -В и А.
Уравнение ВД: -5х + 2у + С = 0 общее.
Для определения слагаемого С подставим координаты точки В.
-5*0 + 2*5 + С = 0, отсюда С = -10.
Уравнение ВД: -5х + 2у - 10 = 0 общее или с положительным коэффициентом перед х:
Уравнение ВД: 5х - 2у + 11 = 0 общее.
в) медианы АЕ.
Находим координаты точки Е как середины стороны ВС.
Е = (В(0;5) + С(3;-2))/2 = (1,5; 1,5). А(-2;0)
Вектор АЕ = (3,5; 1,5).
Уравнение АЕ: (х + 2)/3,5 = у/1,5 или с целыми координатами направляющего вектора: (х + 2)/7 = у/3 каноническое.
Найти длину стороны АС и высоты ВD.
|AC| = √(5² + (-2)²) = √(25 + 4) = √29.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C| /√(A² + B²)
Подставим в формулу данные: В(0;5), AC: 2х + 5у + 4 = 0
d = |2·0+ 5·5 + 4| √(2² + 5²) = |0 + 25 + 4| /√(4 + 25) =
= 29 /√29 = √29 ≈ 5.38516.
Вычислить площадь данного треугольника.
Можно применить .
Есть сторона АС = √29 и высота ВД = 4√29/29.
S = (1/2)√29*√29 = 14,5.
Есть формула площади треугольника прямо по координатам вершин:
Площадь треугольника ABC
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 14,5.