2√153 см ≈ 24,74 см
Объяснение:
1) 24 - це довжина гіпотенузи; а тому кут, який вона утворює з прямою дорівнює 45°, то обидва катета (один з них - довжина проекції, а інший-висота, відстань від точки до прямої) рівні. Приймемо довжину катета за х.
Тоді, згідно з теоремою Піфагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Довжину другої похилої L знаходимо також за теоремою Піфагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
Відповідь: 2√153 см ≈ 24,74 см
1) 24 - это длина гипотенузы, а т.к. угол, который она образует с прямой равен 45°, то оба катета (один из них - длина проекции, а другой - высота, расстояние от точки до прямой) равны. Примем длину катета за х.
Тогда, согласно теореме Пифагора:
х² + х² = 24²
2х²=576
х² = 288
х = √288 см
2) Длину второй наклонной L находим также по теореме Пифагора:
L = √(18² + (√288)²) = √(324 + 288) = √612 = 2√153 ≈ 24,74 см
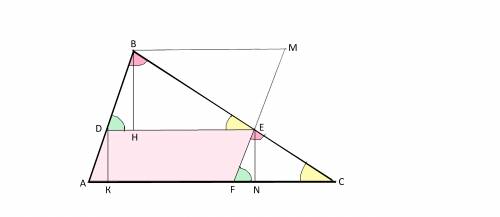
Проведем через вершину В прямую параллельно АС,
продолжим FE до пересечения с нею. Точку пересечения обозначим М.
ВМ||D
EDB||ME
DBMЕ - параллелограмм, площадь которого равна 2S ᐃDBE, т.к. диагонель ВЕ делит его пополам. Очевидно, что площади параллелограммов с равной стороной относятся как отношения их высот, проведенных к этой равной стороне.
SDBME:S ADEF= ВН*DE:DK*DE=48:36=4:3
ВН:DK=4:3
Треугольники DBЕ и FEC подобны, т.к. имеют равные углы по свойству параллельных прямых и секущей.
DK=EN, они - перпендикуляры между параллельными прямыми.
Следовательно, высоты подобных треугольников DBЕ и FEC относятся как 4:3.
Площади подобных фигур относятся как квадраты коэффициентов подобия их линейных размеров.
S Δ DBЕ : Δ S FEC =(4/3)² =16/9
Пусть S Δ FEC=х
24:х=16/9
х=13,5
S Δ FEC=13,5 см²
Площадь Δ АВС равна сумме площадей трех фигур: параллелограмма и двух треугольников.
S Δ ABC=36+24+13,5=73,5 см²