Очевидно что трапеция равнобедренная по правилу(Если трапецию можно вписать в окружность, то она равнобедренная.)
в трапеции(равнобедренной) сумма оснований равна сумме боковых сторон(В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.) отсюда одно из оснований равно 13+13-8=18 см
Далее, из угла меньшего основания опускаем высоту на большее основание. Получаем прямоугольный треугольник, гипотенуза которого равна 13 см, один катет ---5 см, а второй катет ---диаметру вписанной окружности. Далее по теореме Пифагора находим искомый радиус:
R = 6см.
Или воспользоватся формулой что радиус вписанной окружности равен квадратному корню из перемноженных оснований делённый пополам т.е корень из 18*8/2=корень из144/2=12/2=6 см
а) Любой прямоугольный треугольник можно разрезать на два равнобедренных треугольника.
Верно.
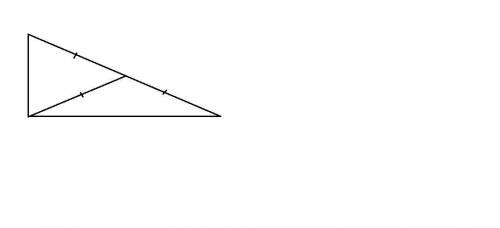
В любом прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине (см. рисунок). Если разрезать треугольник по медиане, то получим два равнобедренных треугольника.
б) Существует четырехугольник со сторонами 2, 3, 5, 11.
Неверно.
Каждая сторона четырехугольника должна быть меньше суммы остальных его сторон.
В данном четырехугольнике для стороны 11:
11 < 5 + 3 + 2 - неравенство неверно, значит четырехугольник с такими сторонами не существует.
в) В любом выпуклом пятиугольнике всегда есть тупой угол.
Верно.
Сумма углов выпуклого многоугольника определяется по формуле:
180°(n - 2), где n - количество сторон.
Для пятиугольника:
180° · 3 = 540°.
Если предположить, что все его углы острые (меньше 90°), то сумма будет меньше 90° · 5 = 450°. Значит есть тупой угол.
г) Внутри любого треугольника существует точка, равноудаленная от всех его вершин.
Неверно.
Точка, равноудаленная от всех вершин треугольника, - это центр описанной окружности.
Только в остроугольном треугольнике центр описанной окружности лежит внутри треугольника. В прямоугольном - на стороне (середина гипотенузы). В тупоугольном - вне треугольника.
обозначим неизвестное основание a; суммы противоположных сторон описанного четырехугольника равны
b + 8 = 13 + 13; b = 18;
Отсюда проекция боковой стороны на большое основание равна (18 - 8)/2 = 5;
Если провести высоту из вершины малого основания, то получается прямоугольный треугольник с катетом 5 и гипотенузой 13. То есть ПИФАГОРОВ ТРЕУГОЛЬНИК 5,12,13.
Высота трапеции равна корень(13^2 - 5^2) = 12.
Осталось сообразить, что вписанная в трапецию окружность касается двух параллельных оснований, поэтому расстояние между ними - то есть высота трапеции - равно диаметру, откуда радиус равен 6;