54°
Объяснение:
Сумма углов в треугольнике равна 180°
Углы при основании равны между собой.
(180°-72°)/2=108:2=54°
Площадь трапеции S=156 см²
Объяснение:
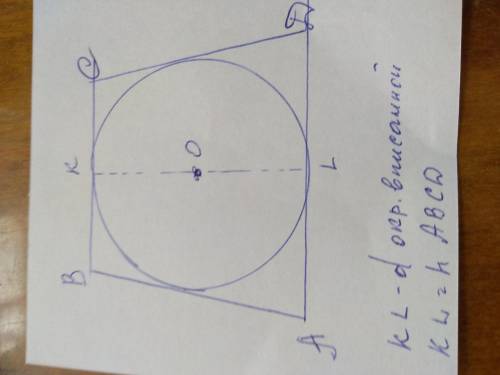
Окружность можно вписать в трапецию тогда и только тогда, когда сумма ее боковых сторон, равна сумме оснований т,е AB+CD= AD+BC
13+13=26см ( AD+BC ), отсюда - сумма оснований AB+CD=26см,
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
S=(а+b):2*h
Высота равнобокой трапеции АВСD равна диаметру вписаной окружности. Зная длинну вписанной окружности в трапецию АВСD, найдем ее диаметр по формуле: P=πd , где P-длинна окружности, которая по условию задачи равна 12πсм.
Подставляем известные значения в формулу и находим диаметр:
12π= πd
d =12π:π; d=12см
Площадь трапеции S=26:2*12=156 см²
Заданная сторона АВ, О - точка пересечения медиан, S - площадь треугольника АВС.
Тогда площадь треугольника АОВ равна S/3,
а стороны АО = 18*(2/3) = 12, ВО = 24*(2/3) = 16, АВ = 20.
Очевидно, что АОВ - "египетский" треугольник (то есть прямоугольный треугольник, подобный треугольнику со сторонами 3,4,5, коэффициент подобия равен 4), поэтому его площадь равна 12*16/2 = 96, а площадь АВС S = 96*3 = 288
Что вы там у Гоши68 нашли неправильного? Все он верно сделал, просто написал без пояснений. Другое дело, что можно было бы заметить, что АОВ - прямоугольный треугольник, но и без этого все равно решение верное.
Вообще-то, я хочу пару слов сказать тут тем, кто серьезно готовится к экзаменам. Если вы применяете такую вещь, как формула Герона - вы должны быть готовы на ходу её вывести, если преподаватель потребует. И не только её, а еще и кучу сопутствующих формул вроде малоизвестной теоремы тангенсов ... А это намного сложнее и длинее, чем эта детская задачка.
Решение: Если один из углов при основании, то они равны, тоесть 2 угла при основании=2*72=144гр, а так так в сумме все углы треугольника составляют 180 гр, то 3-й угол=180-144=36гр ответ : 72,72,36 Если вершина, то 180-72=108гр(углы при основании), а каждый из них равен, тоесь 108:2=.
Объяснение: