Четырехугольник может быть описан около окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
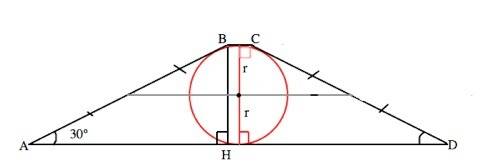
Трапеция - четырехугольник. Сумма оснований описанной трапеции равна сумме боковых сторон и вдвое больше средней линии.
АВ+СD=2•8,5=17 см Трапеция равнобедренная, поэтому АВ=СD=8,5
Угол ВАD=∠СDA= 30°, ⇒ высота ВН трапеции равна половине АВ.
ВН=8,5:2=4,25 см
Диаметр окружности, вписанной в трапецию, перпендикулярен её основаниям и равен её высоте.
R=D:2=4,25:2=2,125 см.
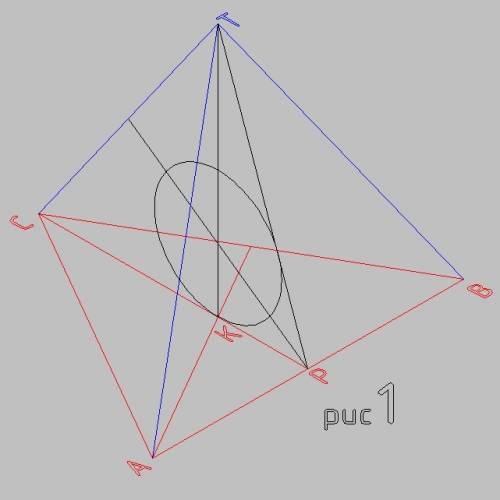
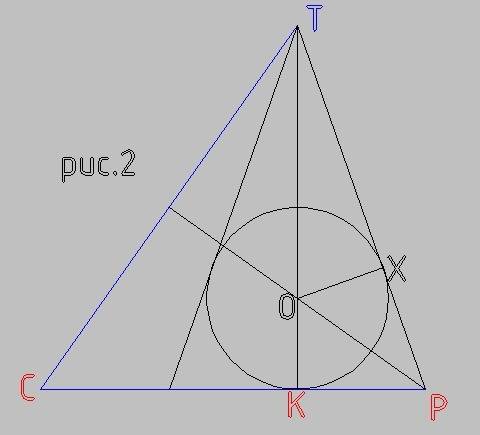
Эту площадь легче всего искать так. Пусть М - середина А1В = √2, поскольку A1T = BT, то ТМ - высота А1ВТ к А1В. ТМ находится из треугольника МАТ, АТ = 1/2; MA =√2/2; => МТ = √3/2;
Площадь А1ВТ = S = А1В*ТМ/2 = √2*√3/4 = √6/4;
отсюда h = 3*V/S = (3/12)/(√6/4) = 1/√6;
Для сравнения - координатный метод дает ответ сам собой.
Уравнение плоскости 2x+y+z =1 пишется сразу (это уравнение плоскости "в отрезках", как оси расположены - очевидно - AD это ось X и так далее); ортогональный вектор (2,1,1) имеет норму √6; то есть уравнение плоскости имеет вид nr = 1/√6; где r = (x,y,z); единичный вектор нормали n = (2/√6, 1/√6, 1/√6); в правой части стоит искомое расстояние от начала координат - точки А (0,0,0) до плоскости.