


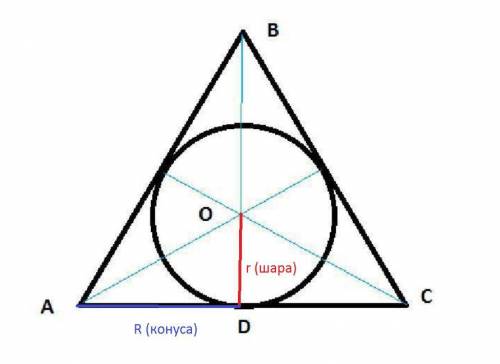
Осевое сечение конуса – равнобедренный треугольник АВС.
АВ=ВС – образующие.
BD– высота конуса, а также высота, медиана и биссектриса равнобедренного треугольника.
О–центр вписанной в треугольник АВС окружности и центр вписанного в конус шара.
ОD=r .
AD=R .
Из прямоугольного треугольника
tg∠OAD = tg(α/2) = r/R . Отсюда r = Rtg(α/2).
ОА– биссектриса угла ВAD, так как центр вписанной в треугольник окружности– точка пересечения биссектрис.
Высота конуса H = R/tg(α/2).
V(шара) = (4/3)πr³ = (4/3)πR³tg³(α/2).
V(конуса)=(1/3)S(осн)·H=(1/3)·πR²·R/tg(α/2) = (1/3)·πR³/tg(α/2).
Разделим V(конуса) на V(шара).
V(конуса) / V(шара) = ( (1/3)·πR³/tg(α/2)) / ((4/3)πR³tg³(α/2)) = 4tg³(α/2)tgα.
ответ: V(конуса) = V(шара) / (4tg³(α/2)tgα).
Высота правильной четырёхугольной пирамиды равна 12 см, а сторона основания равна 24 см. Вычисли двугранный угол при основании.
——————————————————
Основание правильной четырехугольной пирамиды – квадрат.
Все боковые грани правильной пирамиды образуют с плоскостью основания равные углы, а высота проходит через центр основания, который является центром вписанной и описанной около основания окружностей.
Двугранный угол здесь образован радиусом вписанной окружности и апофемой, как отрезками. перпендикулярными ребру основания в одной точке (по т. о трех перпендикулярах).
Радиус вписанной в квадрат окружности равен половине его стороны.
r=24:2=12 (см)
Соединив основание апофемы с центром основания ( основанием высоты пирамиды), получим прямоугольный треугольник.
При этом катеты- высота пирамиды и половина стороны основания - равны 12 см.
Следовательно, треугольник - равнобедренный. Острые углы равнобедренного прямоугольного треугольника равны 45º.⇒ Искомый угол равен 45º.
то AM=3 по условия, а так как радиус у нас равные то BL=3, следовательно BZ=3, и того AB=3+3=6; По теореме радиус окружности равен среднему геометрическому между отрезками которое точка касания делит боковую сторону , то есть r=√CN*ND
r=3, так как Высота ||AB а радиус равен половине высоте =6/2=3
3=√CN*9
CN=1
то есть меньшее основание равна 1+3=4
Площадь равна произведению оснований S=12*4=48