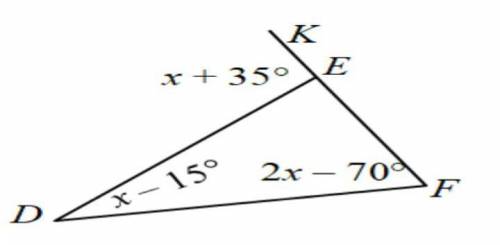
Объяснение:
Внешний угол треугольника равен сумме двух оставшихся углов не смежных с этим внешним углом.
<DEK=<D+<F
Х+35=x-15+(2x-70)
X+35=x-15+2x-70
X-x-2x= - 70-15-35
-2x= - 120
X=60
<D=60-15=45
<F=2×60-70=120-70=50
<E=180-45-50=85
ответ : <D=45 <F=50 <E=85
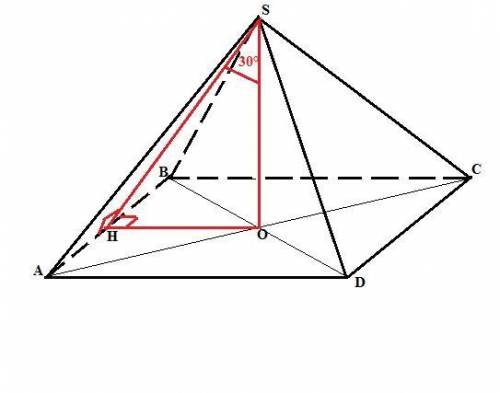
V = 96 см².
Объяснение:
Основание правильной четырехугольной пирамиды - квадрат. Так как углом между наклонной (высота пирамиды) и плоскостью (боковая грань пирамиды) являетс угол между этой наклонной и ее проекцией на плоскость, высота боковой грани (апофема) образует с высотой пирамиды угол 30° (дано). В правильной пирамиде ее вершина проецируется в центр основания (пересечение диагоналей квадрата), расстояние от которого до боковых сторон равно половине стороны квадрата.
Рассмотрим прямоугольный треугольник SOH, образованный апофемой SH (гипотенуза), высотой пирамиды (SO) и половиной стороны основания ОН (катеты). <ОСН=30° (дано).
По Пифагору SO² = SH² - OH².
Так как катет, лежащий против угла 30° равен половине гипотенузы, то SH = 2*OH и тогда SО² = 3*ОН² = 36 см => ОН = 2√3 см.
Сторона основания равна 2*ОН = 4√3, площадь основания равна
So = (4√3)² = 48 см². Тогда
V = (1/3)*So*H = (1/3)*48*6 = 96 см²
Теорема о внешнем угле треугольника:
Величина внешнего угла равна сумме углов треугольника, не смежных с ним.
То есть: