остроугольный и равнобедренный.
Объяснение:
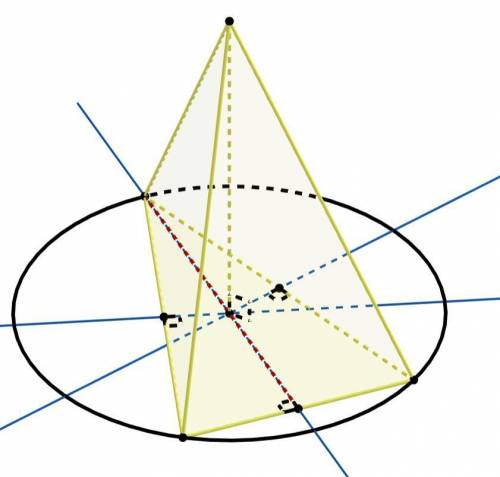
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
Условие написано очень не понятно.
Что такое САО?Треугольник?Угол?
Если угол,то <САО никак не может быть равен 2DBO
Будем считать,что САО и DBO углы<) и они равны между собой
Заданию три недели,его никто не решил,т к не понятно условие
Итак,пересеклись два о резка,по условию задачи
АО=ВО;<САО=<ОВD
<АОС=<DOB,как вертикальные,образованные при пересечении двух отрезков
Следовательно,треугольники САО и DBO равны между собой по второму признаку равенства треугольников,если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника,то эти треугольники равны между собой,а значит
АО=ОВ=5 см
DO=OC=7 cм
DB=AC=6 cм
Периметр-сумма всех сторон треугольника
Периметр САО=5+7+6=18 см
Объяснение:
Объяснение:
8кв.см