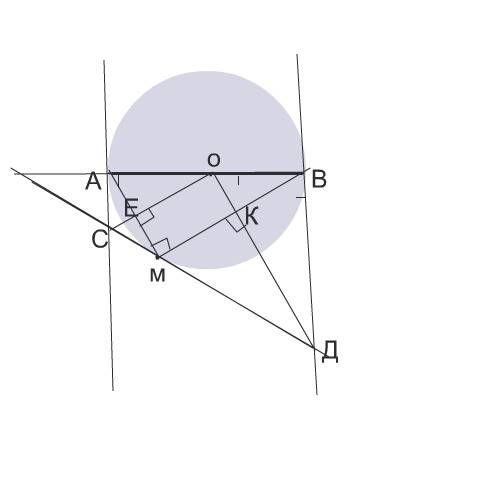
Соединим точку М с концами диаметра АВ.
Получим прямоугольный треугольник АМВ, т.к. угол АМВ опирается на диаметр.
Отрезки АС=СМ и МД=ДВ по скойству отрезков касательных к окружности из одной точки.
следовательно, точки А и М, М и В попарно равноудалены от СО и ОД, являющихся биссектрисами углов, на которых лежит центр вписанной в угол окружности ( в угол АСД и угол СДВ.
Отсюда отрезки ОС и ОД перпендикулярны хордам АМ и МВ.
Теперь расмотрим четырезугоьник ЕМКО.
Угол АМВ - прямой, так как опирается на диаметр.
Углы Е и К тоже прямые. следовательно, угол ЕОК - прямой.
Треугольник СОД - прямоугольный.
1) Находим апофему А как высоту боковой грани.
А = √(6² - (4/2)²) = √(36 - 4) = √32 = 4√2.
Двугранный угол при ребре основания равен плоскому углу между высотами h, проведенными к боковому ребру из точек А и Д в точку М.
По свойству площади треугольника определяем:
А*а = L*h. Отсюда h = А*а/ L = 4√2*4/6 = 8√2/3.
Получаем равнобедренный треугольник с боковыми сторонами АМ и ДМ по 8√2/3 и с основанием АД, равным диагонали квадрата основания 4√2.
Косинус искомого угла М равен:
cos М = ((8√2/3)² + (8√2/3)² - (4√2)²)/(2*(8√2/3)*(8√2/3)) = -1/8.
Угол равен arccos(-1/8) = 1,696 радиан или 97,18 градуса.
2) Угол между плоскостями АВС и BDC1 равен плоскому углу между отрезками, проведенными из точек С и С1 в точку О пересечения диагоналей нижнего основания .
СО = √((2/2)² + (3/2)²) = √(1 + (9/4)) = √13/2.
ответ: tg(COC1) = CC1/CO = 4/(√13/2) = 8/√13 = 8√13/13.
Треугольники СМО и САО равны (ну, например, по трем сторонам :)), поэтому СО - биссектриса угла МОА. Аналогично - из равенства треугольников MOD и ODB - OD - биссектриса угла МОВ. Поэтому СО и OD - биссектрисы смежных углов. ПОэтому они перпендикулярны, чтд.
Если кому-то :) кажется сложным утверждение про биссектрисы смежных углов, сумма углов СМО и МОD равна половине суммы углов МОА и МОВ, то есть 180/2= 90 градусов. По-существу, это и есть доказательство того, что биссектрисы смежных углов взаимно перпендикулярны