можно на русском
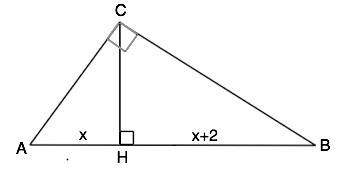
Высота СН прямоугольного треугольника АВС делит гипотенузу АВ на отрезки АН (проекция катета АС) и ВН (проекция катета ВС),
По условию ВН=АН+2 и ВС:АС=3:2
Катет прямоугольного треугольника есть среднее среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. ⇒
АС²=АВ•АН
ВС²=АВ•ВН
Примем АН=х, тогда ВН=х+2, и АВ=2х+2
АС²=АВ•х
ВС²=АВ•(х+2)
ВС:АС=3/2, следовательно, ВС²:АС²=9:4 =>
АВ•(х+2):АВ•х=9:4 =>
( х+2):х=9:4, откуда
5х=8, х=1,6
АВ=2•1,6+2=5,2 (ед. длины)
1)
в равностороннем цилиндре диаметр основания D равен высоте h
Площадь осевого сечения равностороннего цилиндра равна S=4 см2
осевое сечение - квадрат со стороной b=D=h
тогда b^2 = D^2 =S =4 см2
D^2 = 4
D = 2 см ; R=D/2=2/2=1 см
площадь основания цилиндра
So=pi*R^2=pi*1^2=pi =π
ОТВЕТ площадь основания цилиндра = π
2)
Диагональ сечения цилиндра, параллельного оси, равна d=8√3 ,
она наклонена к плоскости основания под углом <A=60º
высота цилиндра h =d*sinA =8√3*√3/2=12
основание сечения b = d*cosA =8√3*1/2=4√3
основание сечения и два радиуса R образуют равнобедренный треугольник
вершина -угол 120º
по теореме косинусов
b^2 = R^2+R^2 -2R*R*c0s120
b^2 = 2*R^2 -2R^2*c0s120
b^2 = 2*R^2 (1 -c0s120)
R^2 = b^2 /(2*(1-c0s120))
R = 4√3 √ ( 1/(2*(1-c0s120)) ) = 4
диаметр основания D=2R=2*4=8
площадь осевого сечения цилиндра.
So=D*h=8*12=48
ОТВЕТ Б)48
3)
б) цилиндрическая поверхность называется боковой поверхностью цилиндра
...........,.....................