Задача: Знайти радіус кола, вписаного в рівносторонній трикутник, якщо радіус кола, описаного навколо цього трикутника, дорівнює 16 см.
Рішення:
Формула кола, вписаного в рівносторонній трикутник:
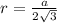, де а — сторона правильного тр-ка
Знайдемо сторону а через формула кола, описаного навколо рівностороннього тр-ка:
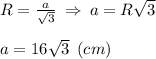
Підставимо значення у формулу кола, вписаного в рівносторонній тр-к
Відповідь: Радіус кола, вписаного в рівносторонній трикутник, рівний 8 см.
Задача: Точка перетину висот BK і PH трикутника BEP є центром вписаного в нього кола. Доведіть, що тр-к BEP рівносторонній.
Рішення:
Центром вписаного в коло трикутника є перетин бісектриса тр-ка, отже і BK та PH є бісектрисами. Висота є бісектрисою, якщо суміжні сторони рівні.
BK — висота/бісектриса ⇒ PB = EB;
PH — висота/бісектриса ⇒ PB = EP.
Відповідно, PB = EB = EP ⇒ ΔBEP — рівносторонній, що і потрібно було довести.
рассмотрим ∆ AHB - он прямоугольный, <H = 90° <BAH= 20° =>
=> т.к сумма всех углов треугольника равна 180°, то
180-(90+20) = 70° (<HBA)
т.к <HBA и <CBA смежные, то их сумма равна 180°
=> 180-70 = 110° (<CBA)
Рассмотрим ∆ CAB, в нем <C=30°, <CBA=110°
найдем <BAC
180-(110+30) = 40°
Можно было легче решить:
второй
Рассмотрим ∆ HCA - он прямоугольный
<C= 30°, <H= 90° =>
=> <A= 180-(90+30)= 60°
Нам известна одна часть угла A, так что мы отнимим её из <A и получим ту часть, что искали:
60-20= 40°
ответ: 40°
