Окружности:
центр A, радиус 2
центр B, радиус 5
центр C, радиус x
AB=10
Точка касания двух окружностей лежит на линии центров.
Если окружности касаются внешним образом, расстояние между центрами равно сумме радиусов.
Если окружности касаются внутренним образом, расстояние между центрами равно разности радиусов.
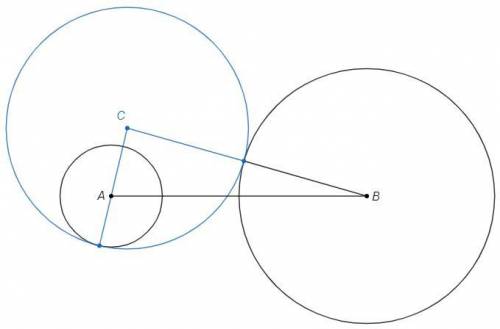
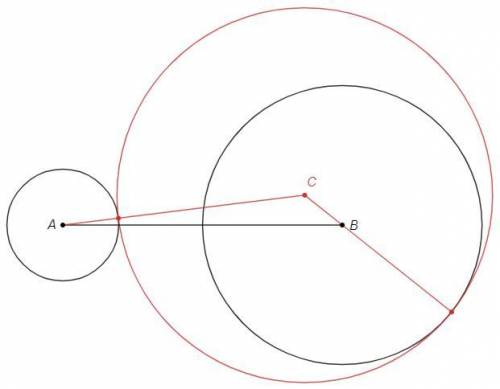
1) Окружность C касается окружности A внутренним образом, а окружности B внешним образом.
AC = |x-2|
BC =x+5
Для трех точек действует неравенство треугольника (ACB). Причем нас устраивает вырожденный треугольник (когда С лежит на AB), поэтому неравенство нестрогое.
AC+BC >= AB
Если x<2, то |x-2|=2-x
Тогда 2-x+x+5 >= 10 <=> 7>=10, противоречие
Следовательно x>=2 и |x-2|=x-2
x-2+x+5 >= 10
x >= (10+2-5)/2
x >= 3,5
2) Окружность C касается окружности A внешним образом, а окружности B внутренним образом.
AC =x+2
BC = |x-5|
Аналогично
x+2+x-5 >= 10
x >= 6,5
Таким образом радиус третьей окружности в любом случае не меньше 3,5.
1)тр.АОВ = трАОМ(прямоуг, общая сторона, угВАО=угОАМ)
АМ=МС=4
АС=8
2)трАВМ-равнобедренный, АО медиана => ВО=ОМ=корень7
3)из трАОВ АО =3(по теор пифагора)
4) cos(угВАО)=3/4, sin(угВАО)=корень7/4
cos(угВАС)= 9/16 - 7/16=1/8
ВС^2=AB^2 + AC^2 -2*AB*AC*cosBAC (по теор косин)
ВС^2=16+64-2*4*8*1/8
ВС=6корень2
5) АD- биссектриса, делящая BD/DC=AB/AC (по св-ву бис)
BD/DC=1/2, BD=1/3*BC=2 корень2
6) из трBDO OD=корень15(по теор пифагора)
AD=3+корень15
ответ: AD=3+кор15; BC=6кор2