





Сначала нужно найти АС и СВ (Так как это катеты соответственно прилежащий и противолежащий углу А) по Теореме Пифагора: (3х)^2+(5x)^2=34^2; 9x^2+25x^2=34^2. Значит, 34х^2 = 34^2. Значит единица измерения сторон треугольника равна \sqrt{34}.
Аналогично найдем, единицу измерения треугольника АСH (3y)^2+(5y)^2=(5sqrt{34})^2
9y^2+25y^2=25*34; 34y^2=25*34; y^2=25; y=5. CH=3y, AH = 5y (Так как это катеты соответственно противолежащий и прилежащий углу А),то CH=15, AH=25. Так как HB = AB - AH, то HB = 34 - 25 = 9.
ответ: BH = 9.
Существует несколько решения такой задачи. В архиве есть два, одно из них мое же, но там задача с несколько иным условием и решена иначе, при желании без труда найдете их.
Вот еще один:
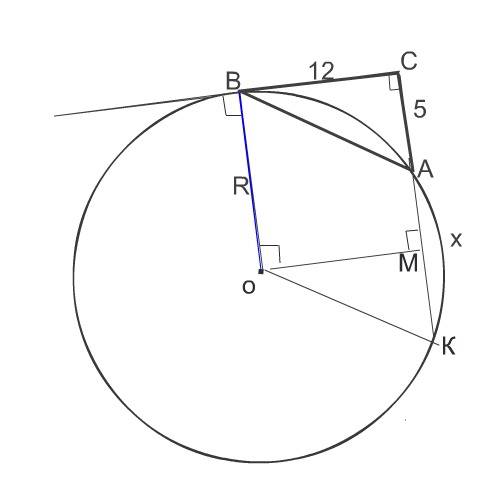
См. рисунок.
Воспользуемся теоремой:
Если из точки вне окружности к ней проведены касательная и секущая, то
квадрат длины отрезка касательной равен произведению всего отрезка секущей к его внешней части.
ВС²=АС*СК
144=5 *(5+х)
144=25 +5х
5х =144-25=119
х=23,8
Проведем перпендикуляры ОВ к точке касания В и ОМ к хорде АК.
Так как треугольник АВС прямоугольный, то ОМ║и =ВС, ОВ║ и=МС
Радиус равен ОВ=МС
Перпендикуляр из центра окружности к хорде делит ее пополам.
R=CК-АК:2=СК-МК
СК=5+23,8=28,8
МК=23,8 :2=11,9
R=28,8-11,9=16,9
ответ: Радиус равен 16,9
√2c^2+2b^2-a^2 = 22
медиана к катету "b"
√2a^2+2c^2-b^2 = 14
по теореме пифагора
a^2+b^2=c^2
решаем систему
{√2c^2+2b^2-a^2 = 22
{√2a^2+2c^2-b^2 = 14
{a^2+b^2=c^2
{2c^2+2b^2-a^2=484
{2a^2+2c^2-b^2=196
{a^2+b^2=c^2
{2(a^2+b^2)+2b^2-a^2=484
{2a^2+2(a^2+b^2)-b^2=196
{4b^2+a^2=484
{4a^2+b^2=196
решая систему получим
a=2√5
b=2√29
площадь квадрата значит равна квадрату гипотенузы , значит
S=(2√5)^2+(2√29)^2 =136