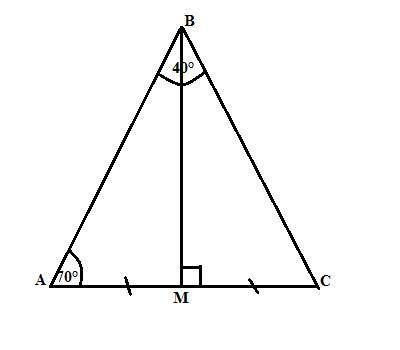
∠МВС = 20°.
∠ВСМ = 70°.
Объяснение:
В треугольнике АВС отрезок ВМ является и высотой (∠ВМА = 90° - дано) и медианой (точка М - середиеа стороны АС - дано). Следовательно, треугольник АВС равнобедренный с основанием АС и отрезок ВМ является биссектрисой (свойство). Тогда
∠МВС = ∠АВС:2 = 40:2 = 20°.
∠ВСМ = ∠ ВАМ = 70° (углы при основании равнобедренного треугольника).
Или так:
∠ВМА=∠ВМС=90° как смежные, равные в сумме 180°.
Прямоугольные треугольники АВМ и СВМ равны по двум катетам: ВМ - общий, а АМ = СМ (так как точка М - середина стороны АС - дано) Из равенства треугольников имеем равенство углов, лежащих против равных сторон:
∠МВС = ∠МВА = ∠АВС:2 = 40:2 = 20°. (∠АВС = ∠МВС + ∠МВА)
∠ВСМ = ∠ ВАМ = 70°.
В любом случае диагональю фигуру разбить на 2 треугольника,
Искомая площадь равна сумме двух треугольников.
Треугольник АВС
Точка А Точка В Точка С
Ха Уа Хв Ув Хс Ус
2 -2 8 -4 8 8
Длины сторон:
АВ ВС АС
6.32455532 12 11.66190379
Периметр Р = 29.98646,
p = 1/2Р = 14.99323,
Площадь определяем по формуле Герона: S = 36.
Треугольник АСД
Точка А Точка С Точка Д
Ха Уа Хс Ус Хд Уд
2 -2 8 8 2 10
АС СД АД
11.6619038 6.32455532 12
Периметр Р = 29.99, р = /2Р = 4.99
Площадь определяем по формуле Герона: S = 36.
Итого площадь фигуры равна 36 + 36 = 72 кв.ед.