Объяснение:
№1
Даны треугольники АВС и А1В1С1 в которых стороны АС и А1С1, высоты ВН и В1Н1 и медианы ВМ и В1М1 равны.
Прямоугольные треугольники НВМ и Н1В1М1 равны по 4-му признаку равенства, так как у них гипотенузы (ВМ и В1М1) и катеты (ВН и В1Н1) равны (дано). => HM=H1M1 и <BMH=<B1M1H1. Значит равны и углы ВМС и В1М1С1 как смежные с равными.
АМ=МС=А1М1=М1С1 как половины равных отрезков АС и А1С1.
Треугольники АВМ и А1В1М1 равны по двум сторонам (АМ=А1М1, ВМ=В1М1) и углу между ними (<BMH=<B1M1H1 - доказано выше) => АВ = А1В1.
Треугольники ВМС и В1М1С1 равны по двум сторонам (МС=М1С1, ВМ=В1М1) и углу между ними (<BMС=<B1M1С1 - доказано выше) => ВС = В1С1.
Тогда треугольники АВС и А1В1С1 равны по трем сторонам, что и требовалось доказать.
Всего в круге 360 градусов.
То есть если пройти 360°, мы окажемся в начальной точке.
1) 360° × 15 = 5400°
Мы 360 градусов 15 раз, оказались в начальной точке.
У нас осталось расстояние в 7°.
Угол в 7° лежит в первой четверти.
Значит, и угол в 5407° лежит в первой четверти.
2) 360° × 69 = 24840°
Мы 360 градусов 69 раз, оказались в начальной точке.
У нас осталось расстояние в 50°.
Стоит минус, значит идём по часовой стрелке.
Угол в -50° лежит в четвёртой четверти.
Значит, и угол в -24890° лежит в четвёртой четверти.
Объяснение:
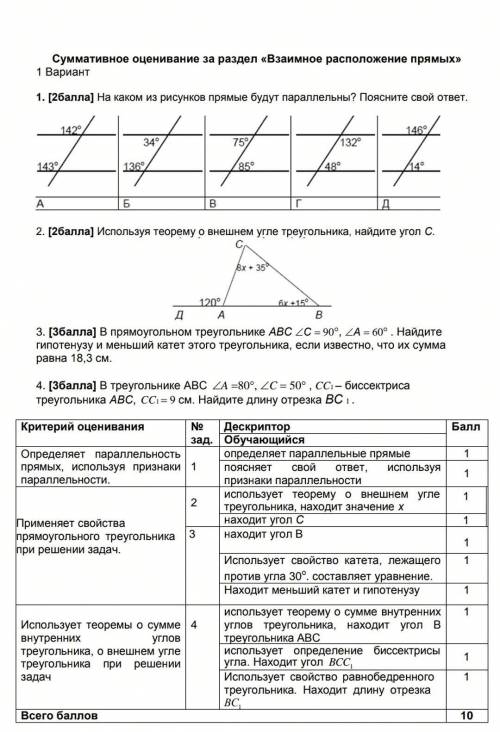
1. Только на рис Г выполняется один из признаков параллельности прямых: сумма односторонних углов 132 + 48 = 180°
2. По теореме о внешнем угле треугольника внешний угол равен сумме двух других углов, не смежных с ним. Составим уравнение на основе данных рисунка:
120 = 8х+35 + 6х+15
14х = 70
х = 5
∠С = 8х + 35 = 8*5 + 35 = 75°
∠В = 6*5 + 15 = 45°
3. ∠ В = 180 - 90 - 60 = 30°
ПО свойству прямоугольного треугольника катет лежащий против угла 30° в два раза меньше гипотенузы. Обозначим меньший катет за х, тогда длина гипотенузы будет 2х. Составим уравнение:
х + 2 х = 18,3
3х = 18,3
х = 6,1 см
гипотенуза = 6,1*2 = 12,2
4. ∠В = 180 - 80 - 50 = 50°
∠ВСС₁ = 50/2 = 25° ⇒
ΔВСС₁ не является равнобедренным, найти ВС₁, зная СС₁, нельзя.