ВМ=1
ВК=1
АМ=4
АР=4
КС=6
РС=6
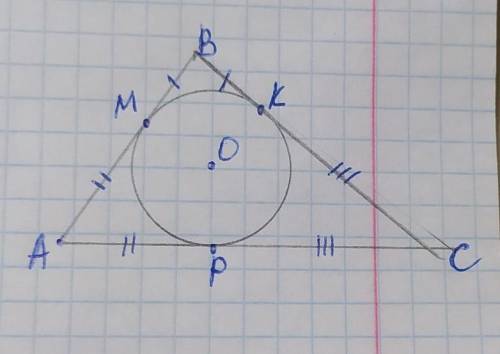
Объяснение:
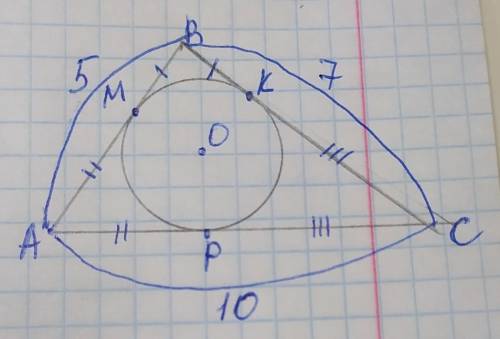
обозначим вершины треугольника А В С, точки касания М, К, Р, а центр вписанной окружности О. Стороны треугольника являются касательными к вписанной окружности, и отрезки касательных соединяясь в одной вершине равны от вершины до точки касания, поэтому: ВМ=ВК, АМ=АР, КС=РС. Пусть ВМ=ВК=х, тогда АМ=РМ=5–х, КС=РС=7–х. В этом случае сторона АС=АР+РС. Составим уравнение:
(5–х)+(7–х)=10
5–х+7–х=10
–2х+12=10
–2х=10–12
–2х= –2
х= –2÷(–2)
х=1
Итак: ВМ=ВК=1, тогда АМ=АР=5–1=4
КС=РС=7–1=6
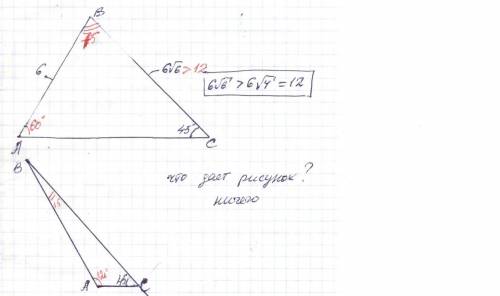
Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение
7
6
9
5
2
4
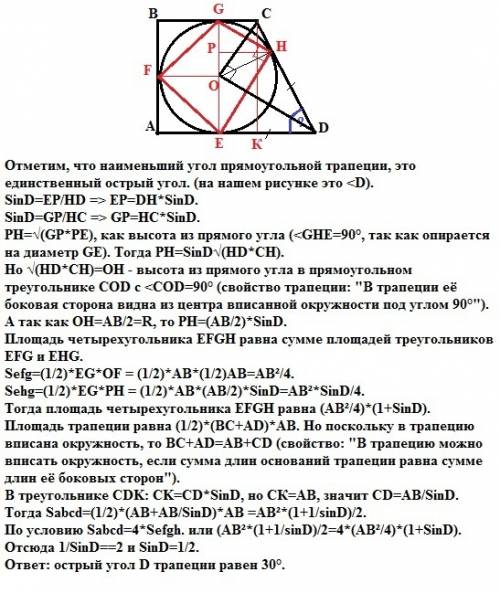
Объяснение: