1 Я думаю что 9, но не знаю как доказать, мы можем взять 2 треугольника, сказать, что у них равны две стороны, основа и одна сторона, но Кута к нет, то есть просто сказать что за тремя сторонами (не уверена)
2 Периметр = 84
Основа =2х
Стороны = 5х и 5х(у равнобедренного треугольника бечные стороны равны)
5х+5х+2х=84
12х=84
Х=7
То есть, основа=2*7=14
Стороны=5*7=35
3 Я не уверена, что-то типа, у меня получился ромб, а у ромба стороны равны, не знаю, вы это ещё не учили, наверное(не уверена)
4 Рассмотрим треугольники АВС и АДС, АС общая, и по два Кута (внутришние одностор) треугольники равны за стороной и 2 углами.(это не уверена) АД- 19см, СД - 11 см, (не уверена Но предполагаю что 30)
5 Не знаю, наверное за основой, как общей, а дальше не знаю
Все на рисунке
, не кидай жалобу, за то что не все решила
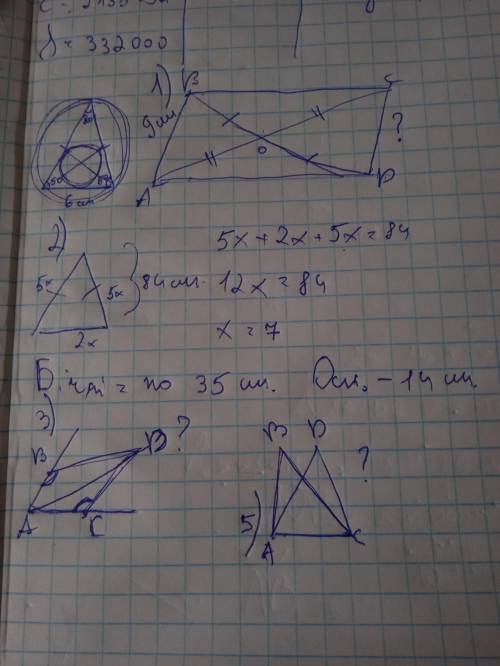
Длины всех сторон двух подобных , но не равных друг другу треугольников целые числа . Чему может быть равен периметр большего , если в одном треугольнике есть длины 2 и 6 , а в другом треугольнике есть сторона длины 3 . Найдите все варианты
Объяснение:
1) В треугольнике с со сторонами 2, 6 , третья сторона может быть равной 5,6,7 согласно теореме о неравенстве сторон треугольника
( если х-третья сторона , то x+2>6 и 6+2>x ⇒ 4<х<8).
2)Тк треугольники подобны и известна одна сторона второго треугольника , то коэффициент подобия может быть равен
а) к=3:2=3/2 , или б) к=3:6=1/2.
Случай а) невозможен для чисел 5,7 из-за условия " Длины всех сторон двух треугольников целые числа...".
Проверим для стороны равной числу 6 : стороны второго треугольника будут равны 6*(3/2)=9 и 2*(3/2)=3. Получили
1 треугольник , стороны 6,6,2 , Р=14 ед,
2 треугольник , стороны 9,9,3 , Р=21 ед.
Случай б) невозможен для чисел 5,7 из-за условия " Длины всех сторон двух треугольников целые числа...".
Проверим для стороны равной числу 6 : стороны второго треугольника будут равны 6*(1/2)=3 и 2*(1/2)=1. Получили
1 треугольник , стороны 6,6,2 , Р=14 ед,
2 треугольник , стороны 3,3,1 , Р=7 ед.
ответ .Периметр большего треугольника 21 ед.
Теорема о неравенстве треугольника " каждая сторона треугольника всегда меньше сумме двух других его сторон."
orjabinina