1. (3Б) AC и BD четырехугольника ABCD пересекаются в точке O, где SAOB = 15 см2, SBOC = 12 см2, SCOD = 8 см2. Найди площадь треугольника AOD. Решение: выполнить построение и отметить известные данные.
По теореме1: S1 ∙ S3 = S2 ∙ S4 вычислить S4.
S4= S1 ∙ S3 / S2
S4 = ………
ответ:
2. (2Б)
В четырехугольнике ABCD точки E, G, F и H – середины сторон AB, BC, CD и AD соответственно. Средние линии EF и GH пересекаются в точке O. Известно, что SAEOH = 14 см2, SEBGO = 16 см2, SOGCF = 20 см2. Найди площадь четырехугольника HOFD.
Решение: выполнить построения.
По теореме2: S1 + S3 = S2 + S4 найти HOFD.
ответ:
геометрия
Пусть х - меньший угол параллелограмма,
х + 16° - больший.
x + x + 16 = 180°
2x = 164°
x = 82°
82° + 16° = 98°
Углы параллелограмма: 82°, 82°, 98°, 98°.
2.
Пусть х - меньшая сторона, 3х - большая сторона.
Р = (x + 3x)·2 = 40
4x = 20
x = 5 см
3x = 15 см
Стороны параллелограмма: 5 см, 5 см, 15 см, 15 см.
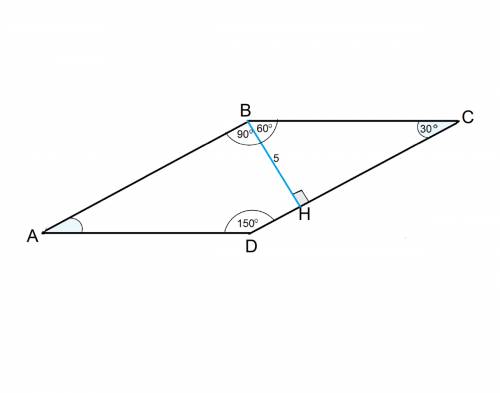
3. В параллелограмме противолежащие углы равны. Сумма углов, прилежащих к одной стороне параллелограмма равна 180°.
∠BAD = ∠BСD = 30°, значит ∠ADC = ∠ABC = 180° - 30° =150°.
ΔBCH: ∠BHC = 90°, ∠BCH = 30°, ⇒
BC = 2CH = 10 см по свойству катета, лежащего напротив угла в 30°.
Противолежащие стороны параллелограмма равны, значит
AD = ВС = 10 см
Периметр 48 см, значит сумма смежных сторон 24 см.
AB = CD = 24 - AD = 24 - 10 = 14 см
ответ: углы 30°, 30°, 150°, 150°
стороны 10 см, 10 см, 14 см, 14 см.