Объяснение:1. Измерение отрезков
Две геометрические фигуры (отрезки, углы,
треугольники и др.) считаются равными, если их
можно наложить друг на друга так, чтобы они совпали.
Отрезки равны, если равны их длины.
Если точка лежит на отрезке , то A B C
+ = .
1. На прямой выбраны три точки , и , причём = 3, = 5. Чему может быть равно ?
(Есть разные возможности.)
B Если точка находится между точками и
A B C
3 5
, то это расстояние равно 3+5 = 8. Но возможен и
другой случай, когда находится вне отрезка .
Нарисовав картинку, убеждаемся, что в этом случае
B A C расстояние равно 5 − 3 = 2. C
3 2
2. На прямой выбраны четыре точки , , ,
, причём = 1, = 2, = 4. Чему может
быть равно ? Укажите все возможности.
B Сначала посмотрим, чему может быть равно
расстояние между точками и . Как и в предыдущей задаче, тут есть две возможности (точка
внутри или вне) | и получается либо 3, либо
1. Теперь мы получаем две задачи: в одной из них
= 3 и = 4, в другой | = 1, = 4.
Каждая имеет по два ответа, так что всего ответов
получается четыре: 4+3, 4−3, 4+1 и 4−1. ответ:
расстояние может равняться 1, 3, 5 или 7. C
3. На деревянной линейке отмечены три деле- 0 7 11
ния: 0, 7 и 11 сантиметров. Как отложить с её отрезок в (а) 8 см; (б) 5 см?
B Используя деления 7 и 11, легко отложить 4
сантиметра. Сделав это дважды, получим отрезок
в 8 сантиметров. Отложить 5 сантиметров немного
сложнее: умея откладывать 8 и 7, можно отложить
1 сантиметр. Сделав это 5 раз, получаем
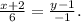
Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А(3; -2).
Получаем: -6*(-3) – 2 + C = 0, следовательно С = 18+2 = 20.
Итого: искомое уравнение: -6х +у + 20 = 0.
Или с положительным коэффициентом перед х:
АН: 6х-у-20 = 0.
Для определения координат точки Н – основания высоты АН треугольника АВС - надо решить систему уравнений прямой ВС и АН:
Больший угол в треугольнике лежит напротив большей стороны.
2√2 > √5, так как (2√2)² = 8, а (√5)² = 5.
Значит, ∠АВС - тупой.
Выясним соответствие остальных углов треугольников.
Если бы ∠КСА был равен ∠ВСА, то отрезок СК проходил бы через точку В, а по условию это не так.
Значит, ∠КСА = ∠ВАС, а ∠АКС = ∠ВСА.
По теореме косинусов, найдем cos ∠BCA:
cos∠BCA = (CB² + CA² - AB²) / (2·CB·CA)
cos∠BCA = (1 + 8 - 5) / (2 · 2√2) = 4/(4√2) = 1/√2 = √2/2
cos∠AKC = cos∠BCA= √2/2