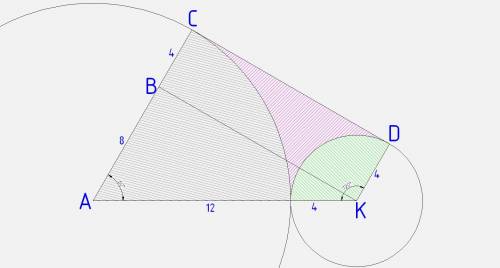
АСДК - трапеция, основания АС=12 см и ДК=4 см
АВ = 12-4 = 8 см
АК = 12+4 = 16 см
По Пифагору
ВК² = АК²-АВ² = 16²-8² = 256-64 = 3*64
ВК = 8√3 см
∠ВАК = arccos(АВ/АК) = arccos(1/2) = 60°
∠ВКА = 90 - ∠ВАК = 30°
∠ДКА = ∠ВКА + 90 = 120°
Полная площадь трапеции
S(ACDK) = 1/2(AC+DK)*BK = 1/2(12+4)*8√3 = 64√3 см²
Площадь сектора большого круга (серая штриховка)
S₁₂ = πR²/360*α = π*12²*60/360 = π*12*12/6 = 24π см²
Площадь сектора малого круга (зелёная штриховка)
S₄ = πR²/360*α = π*4²*120/360 = π*16/3 = 16π/3 см²
И площадь странной фигуры около касательной
S = S(ACDK) - S₁₂ - S₄ = 64√3 - 24π - 16π/3 см²
S = 64√3 - 88π/3 см²
Из прямоугольного ΔАСД:
АД=√(АС²+СД²)=√9+16=√25=5
Опустим высоту трапеции СН из вершины С на основание АД (она же высота ΔАСД, опущенная из прямого угла на гипотенузу)
СН=√АН*НД
Известно, что в равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований
АН=(АД+ВС)/2=(5+ВС)/2
НД=(АД-ВС)/2=(5-ВС)/2
СН²=(5+ВС)/2*(5-ВС)/2=(25-ВС²)/4
Также СН²=СД²-НД²=9-(5-ВС)²/2²=(36-(25-2ВС+ВС²))/4=(11+2ВС-ВС²)/4
Приравниваем
(25-ВС²)/4=(11+2ВС-ВС²)/4
25=11+2ВС
ВС=14/2=7 что невозможно, т.к. ВС<АД
Значит в задаче ошибка какая-то